Завдання 1. Виконати дії:
1. 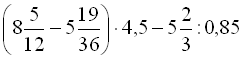 .
.
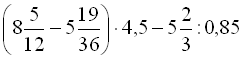 .
.2. 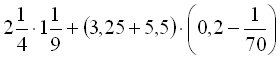 .
.
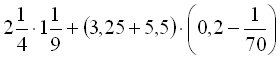 .
.3.  .
.
 .
.4. 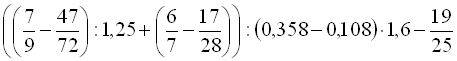 .
.
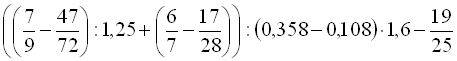 .
.5. 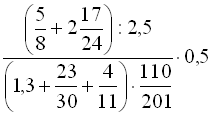 .
.
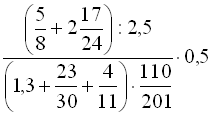 .
.6. 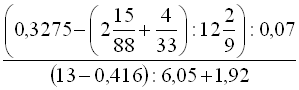 .
.
7. Обчислити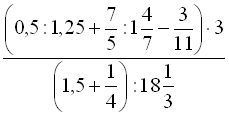 .
.
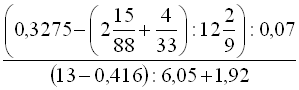 .
.7. Обчислити
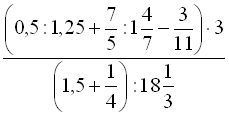 .
.8. Обчислити раціональним способом:
9. Знайти число, якщо 2,5% його дорівнює:
число, якщо 2,5% його дорівнює:  .
.
 .
.10. Знайти число, 5% якого дорівнює сумі чисел 0,5 і 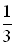 .
.
Завдання 2. Розв’язати текстові задачі:
Завдання 2. Розв’язати текстові задачі:
1. Турист у перший день пройшов 3/5 усього шляху. Скільки кілометрів пройде турист, якщо в перший день він пройшов 15 км? (В: 25 км)
2. Швидкість равлика 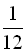 метра за хвилину. Яку відстань проповзе равлик за
метра за хвилину. Яку відстань проповзе равлик за  години? (В:
години? (В:  м)
м)
3. В одному ящику 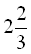 кг яблук, що на
кг яблук, що на  кг менше, ніж в іншому ящику. Скільки кілограмів яблук у двох ящиках? (В:
кг менше, ніж в іншому ящику. Скільки кілограмів яблук у двох ящиках? (В:  кг)
кг)
4. До магазину завезли 900 кг борошна. У перший день продали 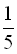 всього борошна, у другий день –
всього борошна, у другий день – 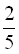 остачі. Скільки кілограмів борошна залишилося продати? (В: 432 кг)
остачі. Скільки кілограмів борошна залишилося продати? (В: 432 кг)
5. Поле було засіяно за три дні. У перший день була засіяна 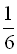 частина всього поля, у другий день –
частина всього поля, у другий день –  усього поля. Яка частина всього поля була засіяна за третій день? (В:
усього поля. Яка частина всього поля була засіяна за третій день? (В:  )
)
6. Басейн наповнюється через першу трубу за 4 години, через другу – за 6 годин. Яку частину басейну залишиться наповнити після спільної роботи обох труб протягом двох годин? (В: 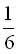 )
)
7. Брат і сестра зробили покупку на 90 грн. Брат заплатив 0,3 вартості покупки, а сестра – решту суми. Скільки грошей заплатила сестра за покупку? (В: 63 грн)
8. Господарка варить вишневе варення, причому на три склянки вишні кладе дві склянки цукрового піску. Скільки цукрового піску потрібно покласти на 12 склянок вишні? (В: 8 склянок)
9. Чисельник звичайного дробу на 3 менше його знаменника. Якщо чисельник цього дробу збільшити на 4, а знаменник – на 8, то даний дріб буде менше отриманого на  . Знайти даний дріб. (В:
. Знайти даний дріб. (В: 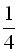 )
)
10. Знаменник звичайного дробу на 4 більше його чисельника. Якщо чисельник цього дробу збільшити на 6, а знаменник – на 5, то отриманий дріб буде на 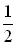 більше даного. Знайти даний дріб. (В:
більше даного. Знайти даний дріб. (В:  )
)
Завдання 3. Знайти х із пропорції:
1. 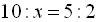 .
.
2.  .
.
3.  .
.
4. 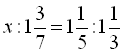 .
.
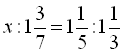 .
.5.  .
.
6. 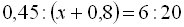 .
.
Завдання 4. Розв’язати задачі на відсотки:
1. Площа поверхні Землі 510,1 мільйона квадратних кілометрів, з них 149,2 мільйона квадратних кілометрів складає суша. Скільки відсотків поверхні Землі покрито водою? В: 70,8 %.
2. З 25 учнів класу на уроці присутні 23. Знайдіть відсоток відвідування. В: 92 %.
3. До 8 кілограмів 70-відсоткового розчину кислоти долили 2 кілограми води. Визначте відсоткову концентрацію нового розчину. В: 56 %.
4. Вкладник поклав до банку 200000 гривень під 7 відсотків річних. Які відсоткові гроші він матиме через 5 років? В: 80,5 тис. грн.
5. Змішали 35-відсотковий розчин кислоти з 10-відсотковим і отримали 300 грамів 20-відсоткового розчину. Скільки грамів 35-відсоткового розчину було взято? В: 120 г.
6. З молока виходить 25 відсотків вершків, а з вершків – 20 відсотків масла. Скільки потрібно мати молока, щоб одержати 10 кілограмів масла? В: 200 кг.
7. Ціна краму спочатку знизилась на 10 відсотків, а потім ще раз на 10 відсотків. На скільки відсотків змінилась вона після двох переоцінок? В: зменшилась на 19 %.
8. Ціна на автомобіль спочатку підвищилась на 20 відсотків, а потім знизилась на 20 відсотків. Як змінилась ціна на автомобіль після цих двох переоцінок? В: зменшилась на 4 %.
9. Скільки кілограмів 20-відсоткового і скільки кілограмів 50-відсоткового сплавів міді потрібно взяти, щоб отримати 30 кілограмів 30-відсоткового сплаву? В: 20 кг і 10 кг.
10. Є 735 грамів 16-відсоткового розчину йоду в спирті. Скільки грамів спирту варто долити до розчину, щоб одержати 10-відсотковий розчин? В: 441 г.
11. Скільки чистого спирту треба додати до 735 грамів 16-відсоткового розчину йоду в спирті, щоб одержати 10-відсотковий розчин?
Завдання 5. Розкласти вирази на множники:
1. 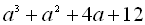 .
.
2.  .
.
3. 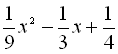 .
.
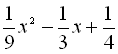 .
.4. 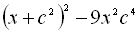 .
.
5.  .
.
6. 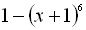 .
.
7.  .
.
8. 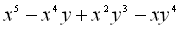 .
.
9.  .
.
10. 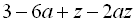 .
.
11. 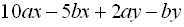 .
.
Завдання 6. Спростити вирази:
1. 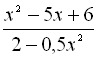 .
.
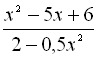 .
.2. 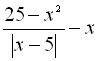 при умові, що
при умові, що 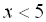 .
.
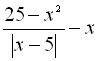 при умові, що
при умові, що 3.  .
.
4. 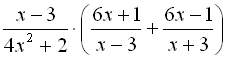 .
.
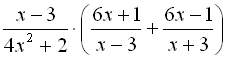 .
.5. 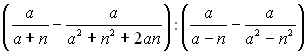 .
.
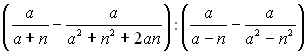 .
.6. 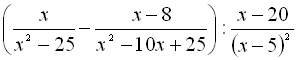 .
.
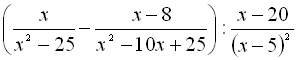 .
.7. 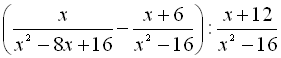 .
.
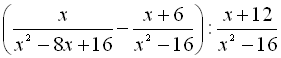 .
.8. 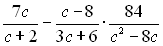 .
.
9. 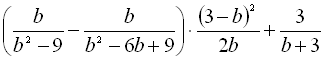 .
.
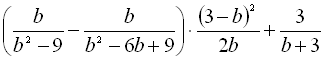 .
.10. 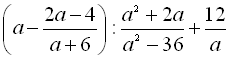 .
.
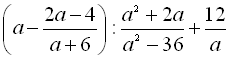 .
.11. 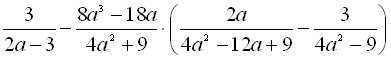 .
.
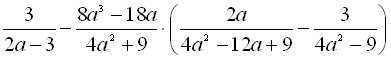 .
.12. 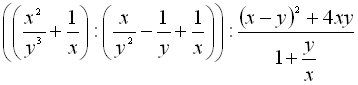 .
.
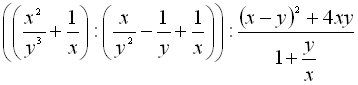 .
.13. Записати вираз у вигляді добутку 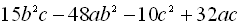 .
.
Завдання 7. Довести, що:
а) значення виразу не залежить від значення змінної:
Завдання 7. Довести, що:
а) значення виразу не залежить від значення змінної:
1. 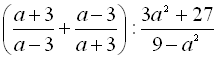 .
.
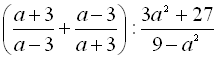 .
.2.  .
.
б) при кожному натуральному значенні п вираз ділиться на 24.
ділиться на 24.
в) різниця квадратів двох послідовних непарних чисел ділиться на 8.
 .
.б) при кожному натуральному значенні п вираз
в) різниця квадратів двох послідовних непарних чисел ділиться на 8.
г) при всіх допустимих значеннях змінної значення виразу не залежить від значення змінної, яка входить в нього: 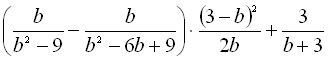 .
.
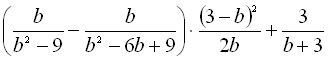 .
.Завдання 8. Розв’язати лінійні рівняння і рівняння, що зводяться до них:
1. 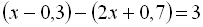 .
.
2. 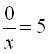 .
.
3. 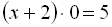 .
.
4. 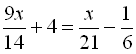 .
.
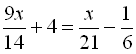 .
.5. 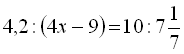 .
.
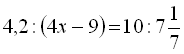 .
.6. 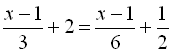 .
.
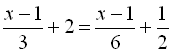 .
.7. 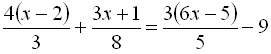 .
.
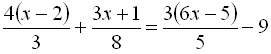 .
.8. 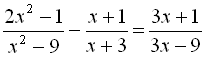 .
.
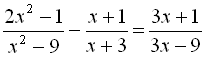 .
.Розв’язати квадратні рівняння і рівняння, що зводяться до них:
1. 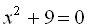 .
.
2. 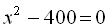 .
.
3. 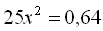 .
.
4. 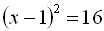 .
.
5. 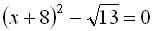 .
.
6. 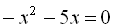 .
.
7. 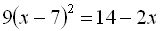 .
.
8. 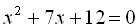 .
.
9. 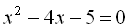 .
.
10. 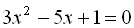 .
.
11. 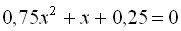 .
.
12. 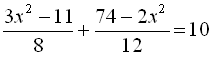 .
.
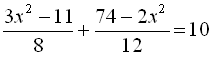 .
.13. 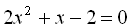 .
.
14. 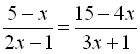 .
.
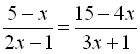 .
.15. 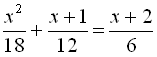 .
.
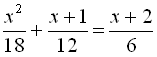 .
.16. 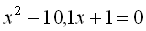 .
.
17. 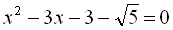 .
.
18. 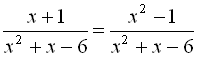 .
.
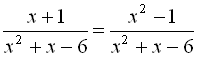 .
.19. 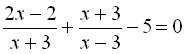 .
.
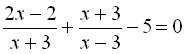 .
.20. 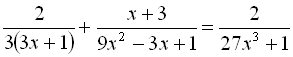 .
.
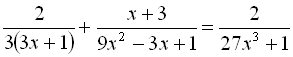 .
.Розв’язати рівняння вищих степенів:
1. 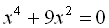 .
.
2. 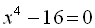 .
.
3. 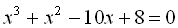 .
.
4. 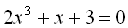 .
.
5. 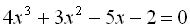 .
.
6. 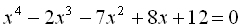 .
.
7. 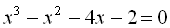 .
.
8. 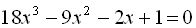 .
.
9. 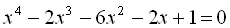 .
.
10. 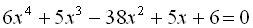 .
.
11. 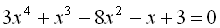 .
.
12. 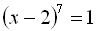 .
.
13. 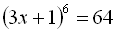 .
.
14. 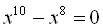 .
.
15. 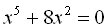 .
.
16. 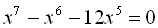 .
.
Розв’язати дробово-раціональні рівняння:
1. 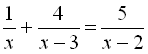 .
.
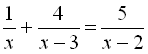 .
.2. 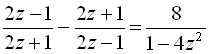 .
.
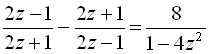 .
.3. 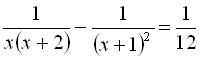 .
.
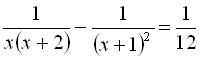 .
.4. 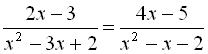 .
.
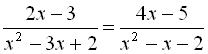 .
.5. 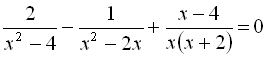 .
.
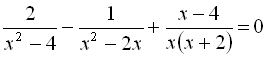 .
.6. 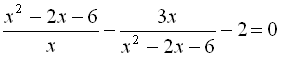 .
.
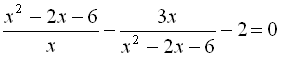 .
.Розв’язати рівняння методом заміни змінної:
1. 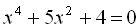 .
.
2. 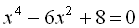 .
.
3. 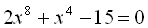 .
.
4. 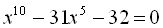 .
.
5. 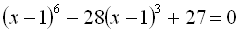 .
.
6. 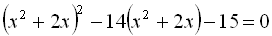 .
.
7. 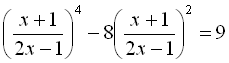 .
.
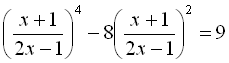 .
.8. 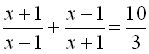 .
.
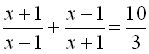 .
.9. 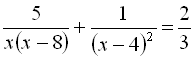 .
.
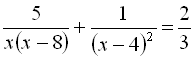 .
.10. 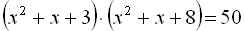 .
.
11. 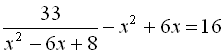 .
.
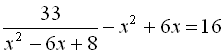 .
.12. 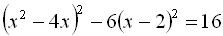 .
.
13. 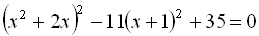 .
.
14. 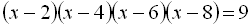 .
.
15. 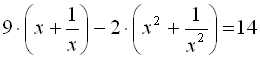 .
.
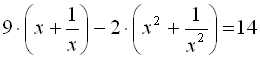 .
.16. 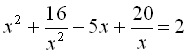 .
.
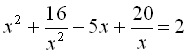 .
.17. 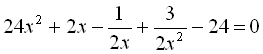 .
.
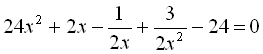 .
.18. 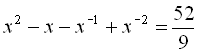 .
.
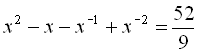 .
.19. 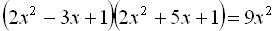 .
.
20. 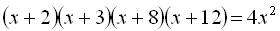 .
.
Розв’язати системи рівнянь:
Рівень А
1. 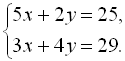
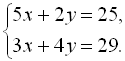
2. 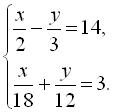
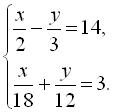
3. 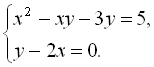
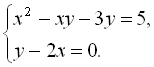
4. 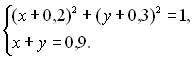
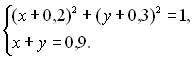
5. 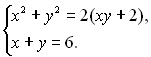
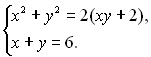
6. 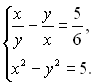
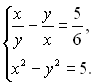
7. 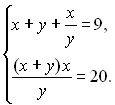
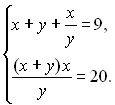
8. 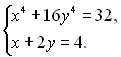
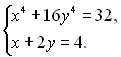
9. 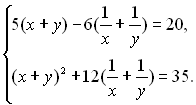
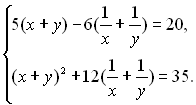
10. 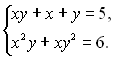
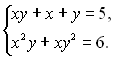
Рівень Б
1. 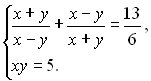
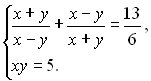
2. 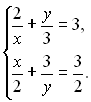
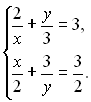
3. 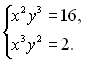
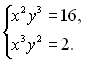
4. 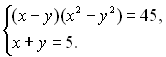
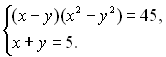
5. 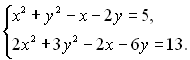
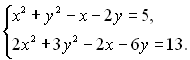
6. 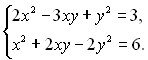
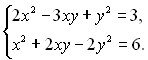
7. 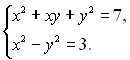
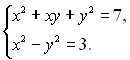
8. 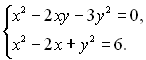
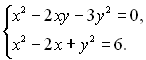
9. 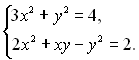
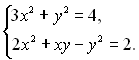
10. 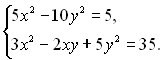
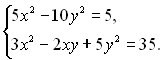
11. 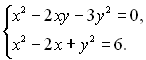
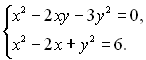
12. 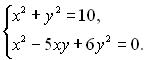
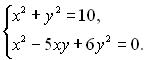
13. 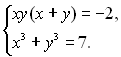
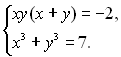
14. 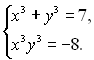
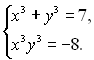
15. 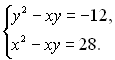
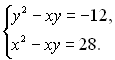
16. 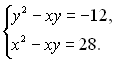
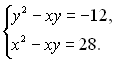
17. 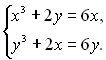
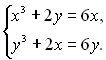
18. 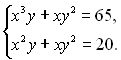
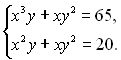
19. 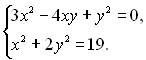
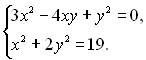
20. 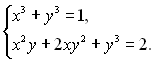
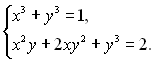
21. 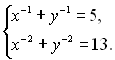
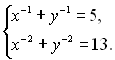
22. 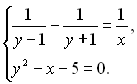
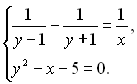
23. 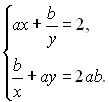
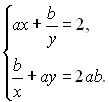
24. 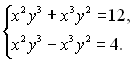
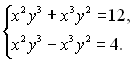
25. 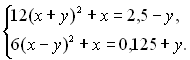
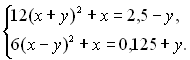
26. 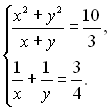
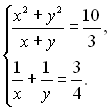
27. 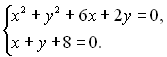
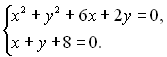
28. Розв’язати рівняння: 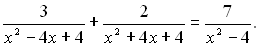
29. Розв’язати рівняння: 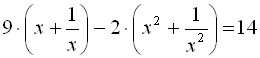 .
.
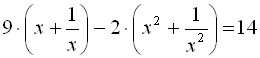 .
.30. Розв’язати систему рівнянь: 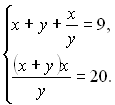
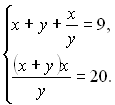
31. Розв’язати сюжетну задачу. Моторний човен проплив 49 км проти течії річки і 8 км по озеру, витративши на весь шлях 2 год. Знайдіть власну швидкість (у км/год.) човна, якщо швидкість течії річки становить 4 км/год.
Завдання 9. Розв’язати нерівності:
Рівень А
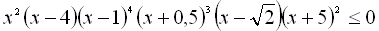 .
.
Рівень А
1. 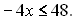
2. 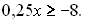
3. 
4. 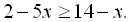
5. 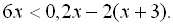
6. 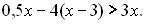
7. 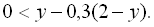
8. 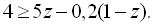
9. 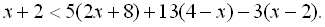
10. 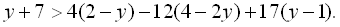
11. 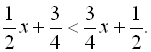
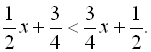
12. 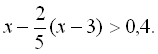
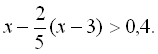
13. 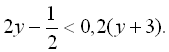
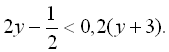
14. 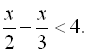
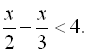
15. 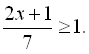
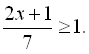
16. 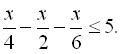
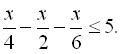
17. 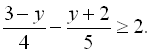
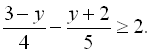
18. 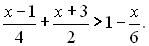
19. 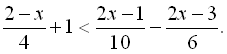
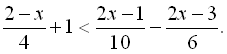
20. 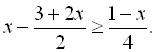
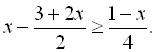
21. 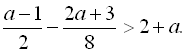
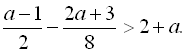
22. 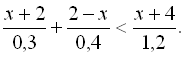
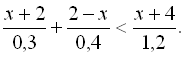
23. 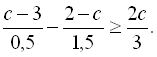
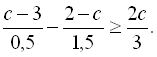
24. 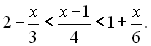
25. 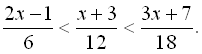
Розв’язати нерівності другого степеня: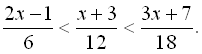
1. 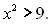
2. 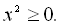
3. 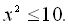
4. 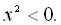
5. 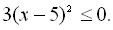
6. 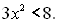
7. 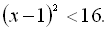
8. 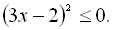
9. 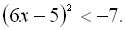
10. 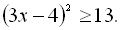
11. 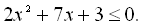
12. 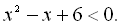
13. 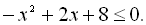
14. 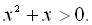
15. 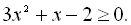
Рівень Б
1. 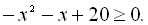
2. 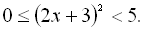
3. 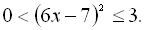
4. 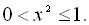
5. 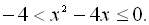
6. 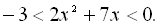
7. 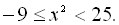
8. 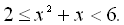
9. 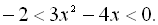
10. 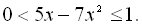
Розв’язати раціональні нерівності методом інтервалів:
Рівень А
1. 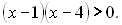
2. 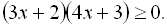
3. 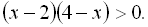
4. 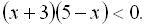
5. 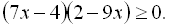
6. 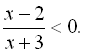
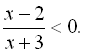
7. 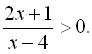
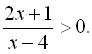
8. 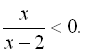
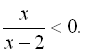
9. 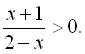
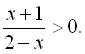
10. 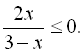
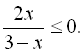
11. 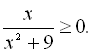
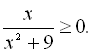
12. 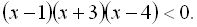
13. 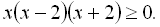
14. 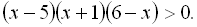
15. 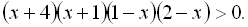
Рівень Б
1. 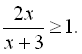
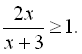
2. 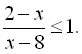
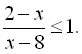
3. 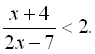
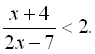
4. 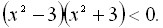
5. 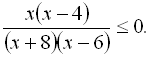
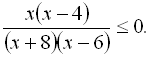
6. 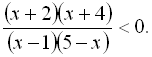
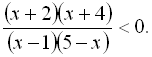
7. 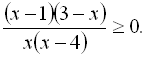
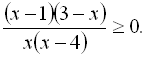
8. 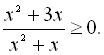
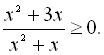
9. 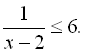
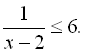
10. 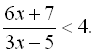
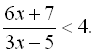
11. 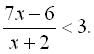
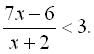
12. 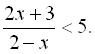
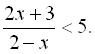
13. 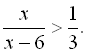
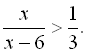
14. 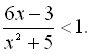
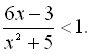
15. 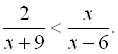
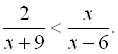
16. 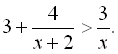
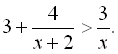
17. 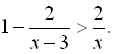
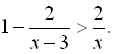
18. 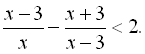
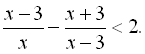
19. 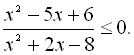
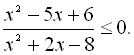
20. 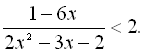
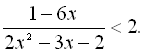
21. 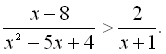
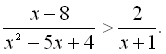
22. 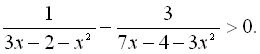
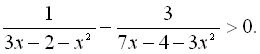
23. 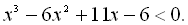
24. 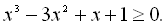
25. 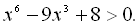
26. 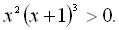
27. 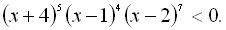
28. 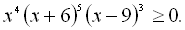
29. 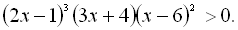
30. 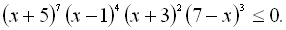
31. 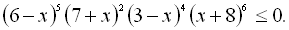
32. 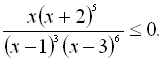
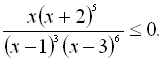
33. 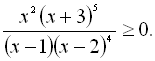
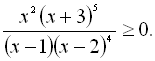
34. 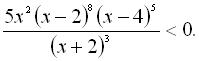
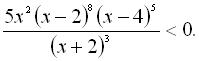
35. 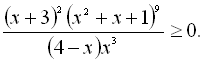
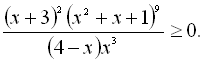
36. 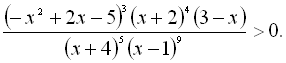
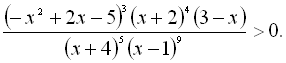
37. 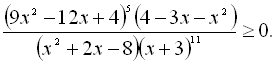
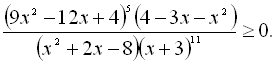
38. 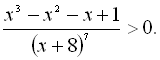
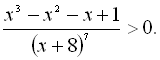
39. 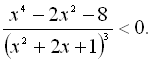
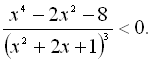
40. 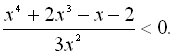
Розв’язати системи нерівностей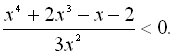
Рівень А
1. 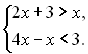
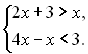
2. 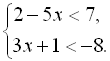
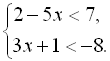
3. 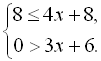
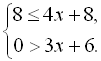
4. 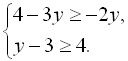
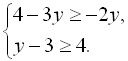
5. 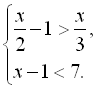
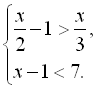
6. 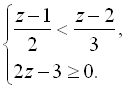
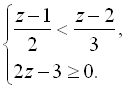
7. 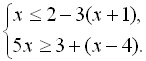
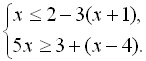
8. 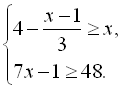
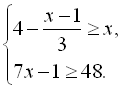
9. 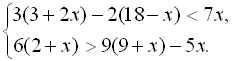
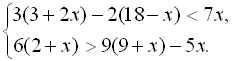
10. 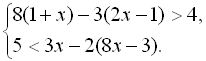
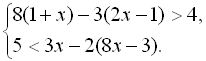
11. 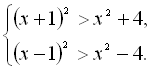
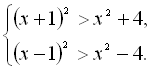
12. 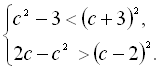
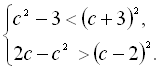
13. 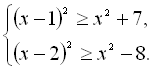
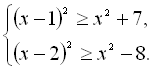
14. 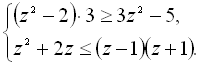
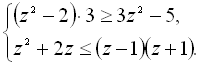
15. 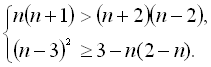
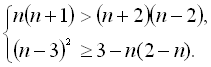
Рівень Б
1. 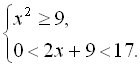
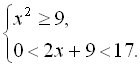
2. 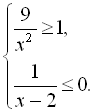
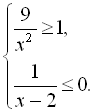
3. 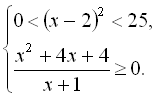
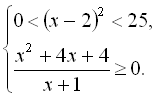
4. 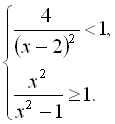
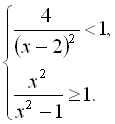
5. 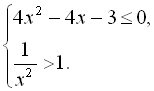
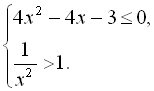
6. 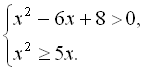
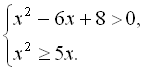
7. 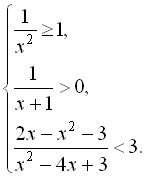
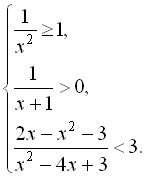
8. 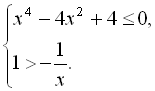
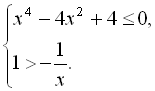
Розв’язати нерівності методом заміни змінної:
1. 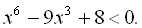
2. 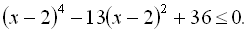
3. 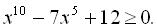
4. 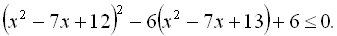
5. 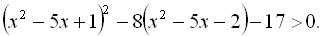
6.Розв’язати нерівність 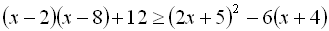 .
.
7. Розв’язати нерівність вищого степеня
8. Розв’язати раціональну нерівність 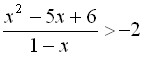 .
.
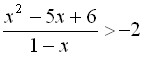 .
.9. Розв’язати систему нерівностей 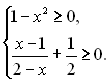
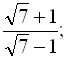
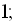
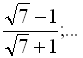 .
.
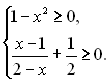
1. Знайти різницю і п-й член заданої арифметичної прогресії:
a) 0; 2; 4; 6; … ;
b) –1; –5; –9; –13; … ;
c) –12; –9; –6; –3; … .
2. Записати перші п’ять членів арифметичної прогресії, якщо 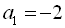 ;
; 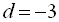 .
.
3. Знайти двадцятий член арифметичної прогресії, якщо її перший член дорівнює 3, а різниця дорівнює 4.
4. Знайти різницю арифметичної прогресії, якщо 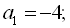
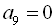 .
.
5. Знайти перший член арифметичної прогресії, якщо 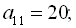
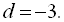
6. Різниця арифметичної прогресії дорівнює 8, сума перших її п’яти членів дорівнює 115. Знайти 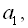
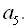
7. Знайти перший член арифметичної прогресії і кількість членів п, якщо 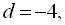
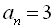 і
і 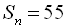 .
.
8. Знайти арифметичну прогресію, якщо: 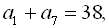
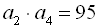 .
.
9. В арифметичній прогресії 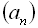 :
: 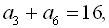
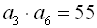 . Скільки членів прогресії треба взяти, щоб отримати суму, рівну 81?
. Скільки членів прогресії треба взяти, щоб отримати суму, рівну 81?
10. Знайти суму перших вісімнадцяти членів арифметичної прогресії 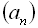 , якщо
, якщо 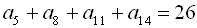 .
.
11. Знайти арифметичну прогресію, якщо сума її п перших членів 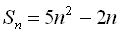 .
.
12. В арифметичній прогресії 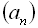 :
: 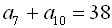 . Знайти
. Знайти 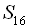 .
.
13. В арифметичній прогресії 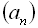 :
: 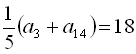 . Знайти
. Знайти 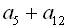 .
.
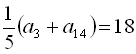 . Знайти
. Знайти 14. В арифметичній прогресії 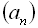 :
: 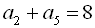 ,
, 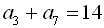 . Знайти прогресію.
. Знайти прогресію.
15. 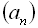 – зростаюча арифметична прогресія,
– зростаюча арифметична прогресія, 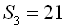 ,
, 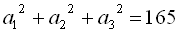 . Знайти
. Знайти 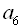 .
.
16. В арифметичній прогресії 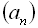 :
: 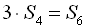 . Знайти
. Знайти 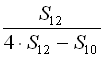 .
.
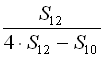 .
.17. Знайти арифметичну прогресію, в якій сума перших трьох членів дорівнює 24, а сума квадратів цих самих трьох членів дорівнює 290.
18. Знайти суму всіх двоцифрових натуральних чисел.
19. Знайти суму всіх додатних парних двоцифрових чисел, що діляться на 3 без остачі.
20. Знайти суму всіх натуральних чисел, кратних 7 і не більших 130.
21. Знайти суму всіх трицифрових натуральних чисел, що при діленні на 3 дають остачу 2.
22. Знайти перший член і різницю арифметичної прогресії, якщо 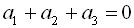 ,
, 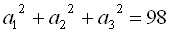 .
.
23. Знайти знаменник і п-ий член заданої геометричної прогресії:
a) 1; 2; 4; 8; …;
b) 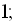
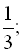
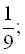
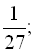 …;
…;
c) 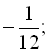 1; -12; 144; … .
1; -12; 144; … .
24. Знайти знаменник геометричної прогресії, якщо 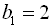 ,
, 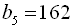 .
.
25. У геометричній прогресії 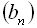 з додатними членами
з додатними членами 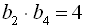 ,
, 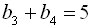 знайти
знайти 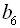 .
.
26. У геометричній прогресії 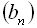 :
: 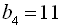 ,
, 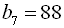 . Знайти
. Знайти 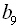 .
.
27. У геометричній прогресії 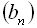 :
: 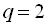 ,
, 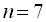 ,
, 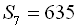 . Знайти
. Знайти 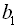 і
і 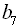 .
.
28. Знайти чотири числа, що утворюють геометричну прогресію, у якій сума крайніх членів дорівнює 27, а добуток середніх дорівнює 72.
29. У геометричній прогресії 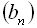 :
: 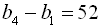 ,
, 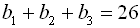 . Знайти
. Знайти 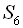 .
.
30. Різниця другого і першого членів геометричної прогресії дорівнює 18, різниця четвертого і третього членів дорівнює 162. Знайти прогресію.
31. Визначити три числа, що утворюють геометричну прогресію з додатними членами, якщо їх сума дорівнює 21, а сума обернених величин дорівнює 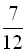 .
.
32. Знайти суму нескінченно спадної геометричної прогресії:
a) 1; 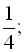
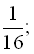
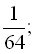 … ;
… ;
b) 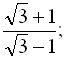 1;
1; 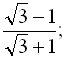 … .
… .
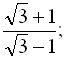 1;
1; 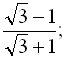 … .
… .33. Визначити суму нескінченно спадної геометричної прогресії 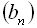 , якщо відомо, що
, якщо відомо, що 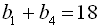 ,
, 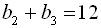 .
.
34. Сума членів нескінченно спадної геометричної прогресії 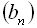 дорівнює 18, а сума квадратів членів тієї ж прогресії дорівнює 108. Знайти
дорівнює 18, а сума квадратів членів тієї ж прогресії дорівнює 108. Знайти 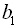 і
і 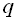 .
.
35. Знайти перший член і знаменник нескінченно спадної геометричної прогресії 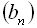 , у якій другий член дорівнює 3, а сума членів дорівнює
, у якій другий член дорівнює 3, а сума членів дорівнює 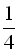 суми квадратів її членів.
суми квадратів її членів.
36. Сума нескінченно спадної геометричної прогресії 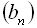
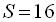 , а сума квадратів усіх її членів
, а сума квадратів усіх її членів 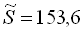 . Знайти четвертий член прогресії.
. Знайти четвертий член прогресії.
37. Сума трьох чисел, що утворюють арифметичну прогресію, дорівнює 21. Якщо до них додати, відповідно, числа 1, 5, 25, то вийдуть три числа, що утворюють геометричну прогресію. Знайти числа, що утворюють арифметичну прогресію.
38. Сума трьох чисел, що є послідовними членами арифметичної прогресії, дорівнює 39. Якщо друге число зменшити на 3, а третє збільшити на 26, то вийдуть три послідовних члени геометричної прогресії. Знайдіть ці числа.
39. Сума трьох чисел, що утворюють зростаючу геометричну прогресію, дорівнює 65. Якщо від меншого з цих чисел відняти 1, а від більшого 19, то отримані три числа утворять арифметичну прогресію. Знайти ці числа.
40. Якщо від чотирьох чисел, що утворюють арифметичну прогресію, відняти, відповідно, 5, 10, 12 і 8, то вийдуть числа, що утворюють геометричну прогресію. Знайти числа, що утворюють арифметичну прогресію.
41. Знайти чотири числа, перші три з яких утворюють геометричну прогресію, а останні три – арифметичну. Сума крайніх чисел дорівнює 14, а сума середніх дорівнює 12.
42. Розв’язати рівняння:
a) 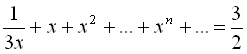 , де
, де 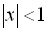 .
.
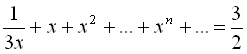 , де
, де b) 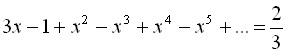 , де
, де 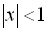 .
.
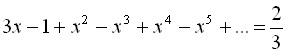 , де
, де 4.7. Орієнтовна контрольна робота № 4
1. Визначити перший член і різницю арифметичної прогресії, якщо 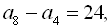
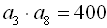 .
.
2. Знайти суму всіх трицифрових натуральних чисел, що діляться на 7 без остачі.
3. У геометричній прогресії 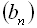 :
: 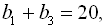
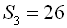 . Знайти прогресію.
. Знайти прогресію.
4. Знайти суму нескінченно спадної геометричної прогресії:
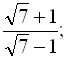
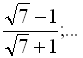 .
.5. Сума трьох перших членів зростаючої арифметичної прогресії дорівнює 15. Якщо від перших двох членів цієї прогресії відняти по одиниці, а до третього члена додати 1, то отримані три числа складуть геометричну прогресію. Знайдіть суму 10 перших членів арифметичної прогресії.
