Зразки перетворення виразів

Формули скороченого множення

Розкладанням многочлена на множники називається перетворення многочлена в добуток двох або декількох многочленів, серед яких можуть бути і одночлени.

Способи розкладання многочлена на множники

1) Винесення спільного множника за дужку. Кожну змінну, яка входить у всі члени многочлена, виносять з найменшим показником, який вона має в даному многочлені: .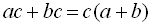

Приклад 1.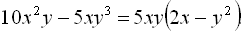 

2) Використання формул скороченого множення.

Приклад 2.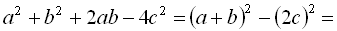 

.

3) Спосіб групування. Він полягає у поєднанні в групи тих членів, які мають спільні множники, за дужки виноситься спільний множник кожної з груп. Якщо після такого перетворення виявиться спільний множник у всіх утворених групах, то його виносять за дужки.

Приклад 3.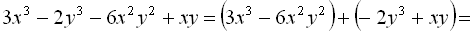 

Розкладання квадратного тричлена на лінійні множники

Якщо 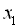 і 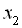 – корені квадратного тричлена  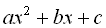(тобто корені рівняння 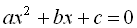), то .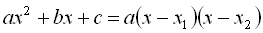

Приклад 4. 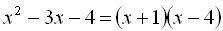, тому що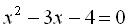  

 .

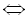
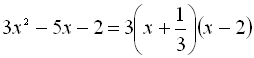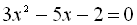
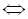
Приклад 5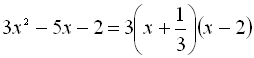. , так як  

 .

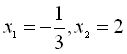Виділення повного квадрата двочлена з квадратного тричлена

Нехай є квадратний тричлен 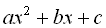 і потрібно перетворити його до виду  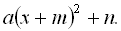Для цього чинимо в такий спосіб: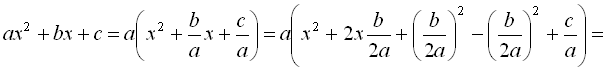 

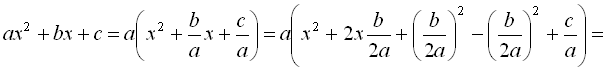
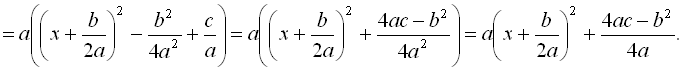     Наведемо приклади на виділення повного квадрата.

Приклад 6.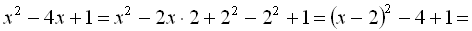 

.

Приклад 7.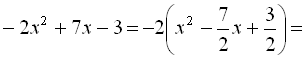 

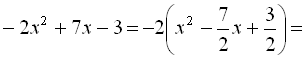
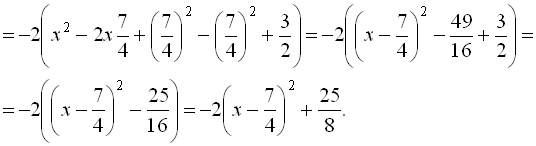
Перетворення цілих раціональних виразів зводиться до віднімання, додавання, множення та піднесення змінних до натурального степеня.

Приклад 8. Як записати вираз у вигляді добутку:

а) 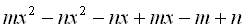; б) .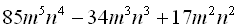

Розв’язання

а)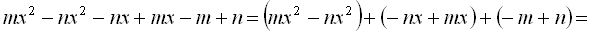 

.

б) .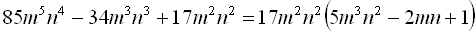

Перетворення дробових раціональних виразів зводиться до віднімання, додавання, множення та ділення раціональних дробів, а також до піднесення дробу до натурального степеня. Будь-який раціональний вираз можна перетворити в дріб, чисельник і знаменник якого – цілий раціональний вираз; в цьому, як правило, полягає мета тотожних перетворень раціональних виразів.

Приклад 9. Спростити вираз

.

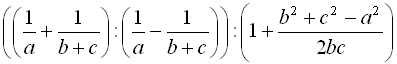Розв’язання

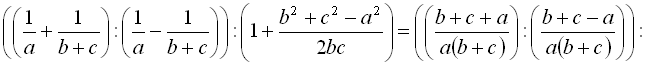
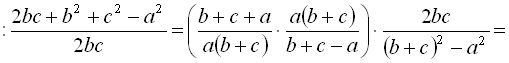
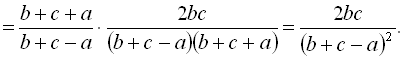
Приклад 10. Спростити вираз

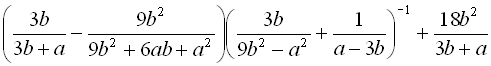
Розв’язання

1) ;

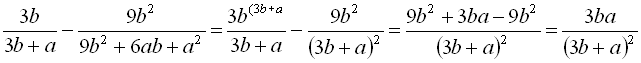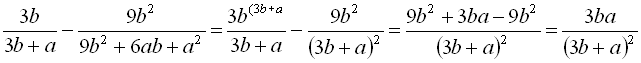2) ;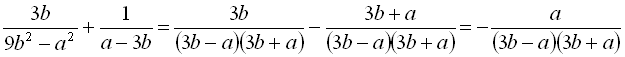

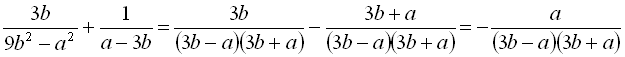3) ;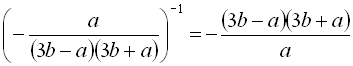

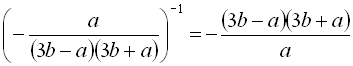4) ;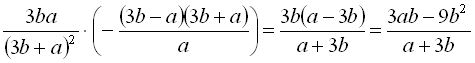

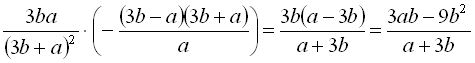5) 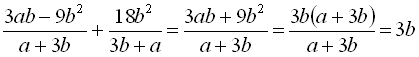.
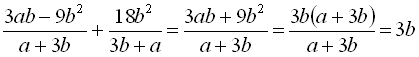