При розв’язуванні систем лінійних нерівностей, що складаються з двох нерівностей, можна зображати розв’язування за допомогою двох числових осей або за допомогою однієї осі, за допомогою дуг або без дуг, без допомоги штриховок або за допомогою штриховок, наносячи штриховки, які мають різний кут нахилу відносно числової прямої, знизу і згори або тільки згори (знизу).
Приклад 1. Розв’язати систему нерівностей і знайти всі її цілі розв’язки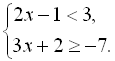 
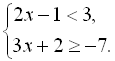
Розв’язання
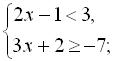
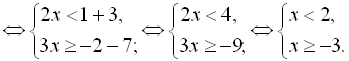
1-й варіант (з використанням двох числових осей):
2-й варіант (з використанням однієї числової осі і штриховок знизу і згори осі):
3-й варіант (з використанням однієї осі, дуг і штриховок).
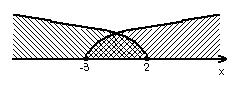
Шукана множина зображена подвійною штриховкою за допомогою накладання двох штриховок.
4-й варіант (з використанням однієї осі і дуг):
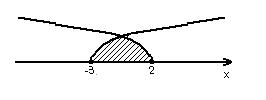
Штриховку наносимо лише там, де задані множини пересікаються.
Цілими розв’язками даної системи є значення – 3 ; – 2; – 1; 0; 1.
Відповідь: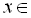 
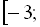
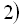; – 3 ; – 2; – 1; 0; 1.
; – 3 ; – 2; – 1; 0; 1.
Приклад 2. Розв’язати нерівність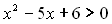 
.
.
Розв’язання
Розв’язавши квадратне рівняння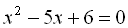 
, одержимо корені 
. Тоді квадратний тричлен розкладеться на такі множники: 
.
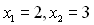, одержимо корені . Тоді квадратний тричлен розкладеться на такі множники: .
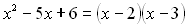Звідси,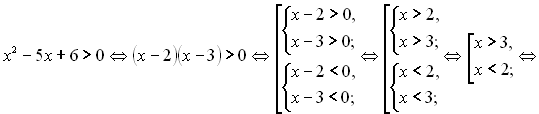 
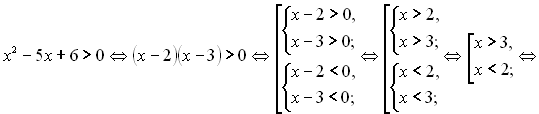
Відповідь: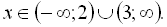
Квадратні нерівності, а також нерівності вищих степенів можна розв’язувати методом інтервалів (методом проміжків). В його основі лежить така властивість двочлена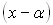 
: точка 
ділить числову вісь на дві частини – праворуч від точки ? двочлен 
, а ліворуч від точки ? 
.
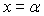: точка ділить числову вісь на дві частини – праворуч від точки ? двочлен 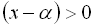, а ліворуч від точки ? .
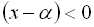Приклад 3. Розв’язати нерівність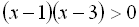 
.
.
Розв’язання
Многочлен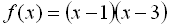 
перетворюється в нуль у точках 
Ці точки розбивають координатну пряму на проміжки (
1),
перетворюється в нуль у точках 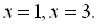Ці точки розбивають координатну пряму на проміжки ( 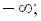1),
(1; 3), (3;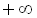 
), усередині кожного з яких функція 
зберігає знак.
), усередині кожного з яких функція 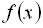зберігає знак.
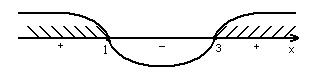
Оскільки в проміжку (3;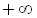 
) співмножники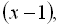 
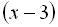додатні, то їхній добуток додатний, тобто 
. Відзначимо проміжок (3; 
) знаком “+”. Далі знаки в проміжках чергуються. Проводимо через визначені точки “криву знаків”. На тих проміжках, де ставиться знак “+”, виконується нерівність 
; на тих проміжках, де знак “– “, виконується нерівність 
. Отже, розв’язком початкової нерівності є об’єднанням проміжків: (
1), (3; ).
) співмножники додатні, то їхній добуток додатний, тобто 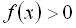. Відзначимо проміжок (3; 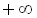) знаком “+”. Далі знаки в проміжках чергуються. Проводимо через визначені точки “криву знаків”. На тих проміжках, де ставиться знак “+”, виконується нерівність 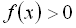; на тих проміжках, де знак “– “, виконується нерівність 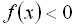. Отже, розв’язком початкової нерівності є об’єднанням проміжків: ( 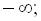1), (3; ).
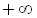Відповідь: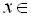 
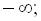( 1)
(3; ).
( 1)(3; ).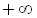
Приклад 9. Розв’язати нерівність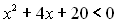 
.
.
Розв’язання
Якщо прирівняти до нуля многочлен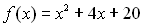 
, то дискримінант виявиться від’ємним. А це означає, що квадратний тричлен додатний при всіх дійсних значеннях змінної х, тому при 
нерівність розв’язків не має.
, то дискримінант виявиться від’ємним. А це означає, що квадратний тричлен додатний при всіх дійсних значеннях змінної х, тому при 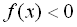нерівність розв’язків не має.
Відповідь: нерівність розв’язків не має.
Приклад 10. Розв’язати нерівність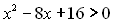 
.
.
Розв’язання
Многочлен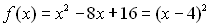 
є невід’ємним при будь-якому дійсному значенні змінної х, тому нерівність 
справджується при всіх дійсних значеннях змінної х, крім 4.
є невід’ємним при будь-якому дійсному значенні змінної х, тому нерівність 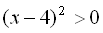справджується при всіх дійсних значеннях змінної х, крім 4.
Відповідь: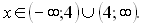 
Приклад 11. Розв’язати нерівність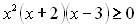 
.
.
Розв’язання
Многочлен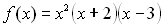 
перетворюється в нуль в точках 
. Ці точки розбивають координатну пряму на чотири проміжки. Оскільки даний многочлен містить множник у парному степені – це 
, то при переході «змійки» через “0” знак не буде змінюватись. Зазначимо, що точка 
входить у множину розв’язків, тому що при 
дістаємо 
.
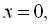
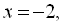
перетворюється в нуль в точках 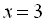. Ці точки розбивають координатну пряму на чотири проміжки. Оскільки даний многочлен містить множник у парному степені – це 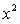, то при переході «змійки» через “0” знак не буде змінюватись. Зазначимо, що точка 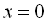входить у множину розв’язків, тому що при 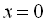дістаємо .
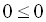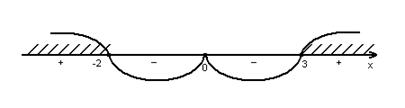
Відповідь: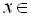 
.
.
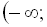
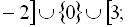
Приклад 12. Розв’язати нерівність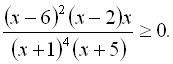 
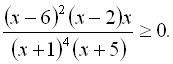
Розв’язання
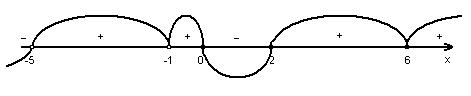
Наносимо точки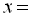 
6; 2; 0; –1; –5 на числову вісь. Відзначимо точки 
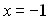і 
, при переході через них «змійки» знаки не будуть змінюватись. За допомогою «кривої знаків» дістаємо розв’язки, які позначені на рисунку зі знаком «+».
6; 2; 0; –1; –5 на числову вісь. Відзначимо точки і 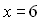, при переході через них «змійки» знаки не будуть змінюватись. За допомогою «кривої знаків» дістаємо розв’язки, які позначені на рисунку зі знаком «+».
.