Розв’язування задач на складання рівнянь можна розбити на кілька етапів:
1) вибір невідомих величин і їх позначення,
2) запис вказаних співвідношень у вигляді рівнянь або систем рівнянь,
3) розв’язання цих рівнянь або системи рівнянь з урахуванням області визначення
(при цьому враховуються природні фізичні обмеження, які звичайно в тексті задач не наведено).
1) вибір невідомих величин і їх позначення,
2) запис вказаних співвідношень у вигляді рівнянь або систем рівнянь,
3) розв’язання цих рівнянь або системи рівнянь з урахуванням області визначення
(при цьому враховуються природні фізичні обмеження, які звичайно в тексті задач не наведено).
Двом друкаркам було доручено деяке завдання. Друга друкарка почала працювати на 1 годину пізніше, ніж перша. Через 3 години після того, як перша друкарка почала роботу, обом їм залишилося виконати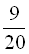 
усієї роботи. Коли завдання було виконано, виявилося, що кожна друкарка зробила половину всієї роботи. За скільки годин кожна друкарка окремо може виконати всю роботу?
усієї роботи. Коли завдання було виконано, виявилося, що кожна друкарка зробила половину всієї роботи. За скільки годин кожна друкарка окремо може виконати всю роботу?Розв’язання
Позначимо через x та y час (у годинах) виконання всієї роботи першою і другою друкаркою відповідно, тоді за 1 год. перша друкарка виконає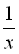 
, а друга – 
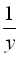частину всієї роботи. За умовою задачі складемо перше рівняння: 
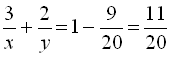. Половину всієї роботи перша друкарка виконала за 
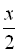год., а друга – за 
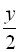год. Оскільки друга друкарка працювала на 1 год. менше, ніж перша, маємо друге рівняння: 
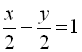. Далі складемо систему 
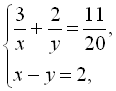і розв’яжемо її:
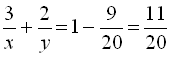, а друга – частину всієї роботи. За умовою задачі складемо перше рівняння: . Половину всієї роботи перша друкарка виконала за 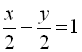год., а друга – за год. Оскільки друга друкарка працювала на 1 год. менше, ніж перша, маємо друге рівняння: . Далі складемо систему 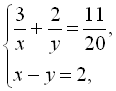і розв’яжемо її:
Умову задачі задовольняють лише значення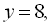 
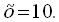
Відповідь: 10 год., 8 год.