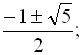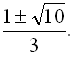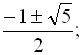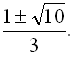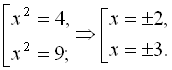Рівняння 3x – 4 = 6 + 3x не має коренів, оскільки при перенесенні невідомих в одну частину, а відомих в іншу – отримуємо неправильну числову рівність:

Рівняння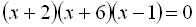 має три корені
має три корені
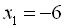 ,
, 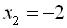 ,
, 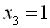 .
. 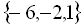 – множина коренів рівняння.
– множина коренів рівняння.

Рівняння
Лінійні рівняння – це рівняння виду:
де а і b – дійсні числа.
Рівняння (1) має один корінь, якщо 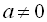 :
: 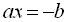 , звідки
, звідки 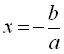 .
.
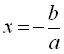 .
.
У рівнянні (1) при 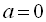 і
і 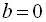 х – будь-яке число.
х – будь-яке число.
Наприклад,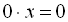
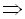
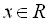 .
.
Наприклад,
У випадку, коли 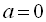 ,
, 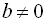 , рівняння розв’язків немає.
, рівняння розв’язків немає.
Наприклад,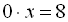
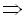
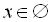 .
.
Наприклад,
Розглянемо лінійні рівняння або ті, що зводяться до лінійних.
Приклад 3. Розв’язати рівняння 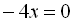 .
.
Розв’язання
Відповідь: 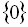 .
.
Приклад 4. Розв’язати рівняння 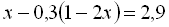 .
.
Розв’язання
Розкриємо дужки і зведемо подібні члени:
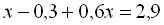
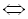
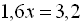
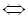
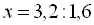
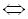
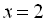 .
.
Відповідь: 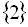 .
.
Приклад 5. Розв’язати рівняння 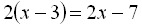 .
.
Розв’язання
Оскільки отримана рівність не є правильною, тому дане рівняння розв’язків немає.
Відповідь: 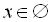 .
.
Приклад 6. Розв’язати рівняння 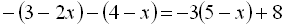 .
.
Розв’язання
Відповідь: 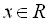 .
.
Приклад 7. Розв’язати рівняння 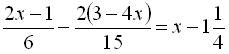 .
.
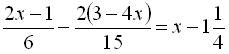 .
.
Розв’язання
Перенесемо все в одну частину і зведемо до спільного знаменника:
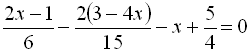
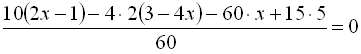
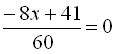
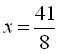 .
.
Відповідь: 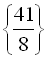 .
.
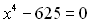
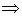
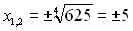 . Часто учні, розв’язуючи такі рівняння, знаходять лише один розв’язок рівняння
. Часто учні, розв’язуючи такі рівняння, знаходять лише один розв’язок рівняння 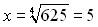 .
.
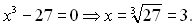
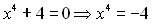 , а це неможливо, тому рівняння розв’язків не має.
, а це неможливо, тому рівняння розв’язків не має.
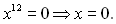
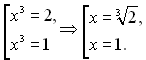

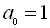 , тому раціональні корені рівняння шукаємо серед чисел ±1,
, тому раціональні корені рівняння шукаємо серед чисел ±1, 
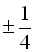 . Перевіряючи ці числа шляхом підстановки у початкове рівняння, знаходимо корінь
. Перевіряючи ці числа шляхом підстановки у початкове рівняння, знаходимо корінь 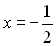 . Звідси, потрібно поділити початковий многочлен лівої частини рівняння на
. Звідси, потрібно поділити початковий многочлен лівої частини рівняння на 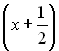 або, що те ж саме, але без дробів, на
або, що те ж саме, але без дробів, на  (тоді ми при діленні уникаємо дробових коефіцієнтів).
(тоді ми при діленні уникаємо дробових коефіцієнтів).



 або
або
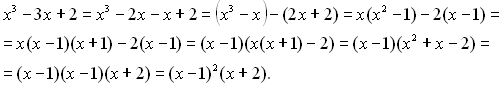
 .,
.,

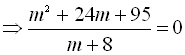
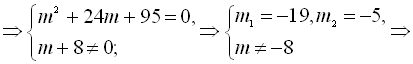
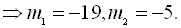
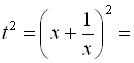

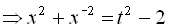 .
.

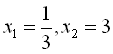 .
.

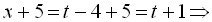 початкове рівняння записується у вигляді
початкове рівняння записується у вигляді 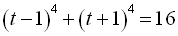 . Застосовуючи трикутник Паскаля, отримуємо
. Застосовуючи трикутник Паскаля, отримуємо
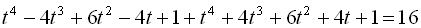
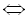
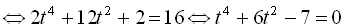 . Розв’язуючи це біквадратне рівняння, дістаємо
. Розв’язуючи це біквадратне рівняння, дістаємо 
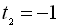 .
.
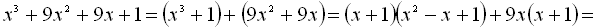
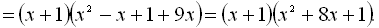
Звідси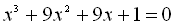
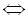
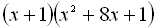
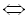
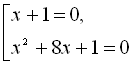
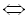
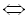
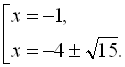
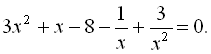 Згрупувавши доданки, маємо
Згрупувавши доданки, маємо
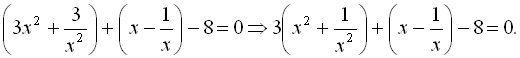
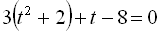
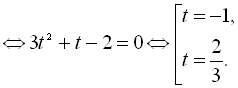
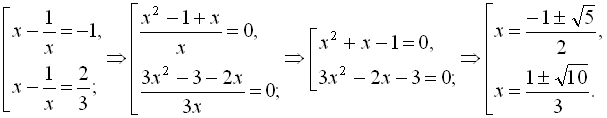
Приклад 8. Розв’язати рівняння 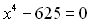 .
.
Розв’язання
Приклад 9. Розв’язати рівняння 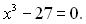
Розв’язання
Відповідь: 3.
Приклад 10. Розв’язати рівняння 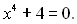
Розв’язання
Відповідь: .
.
Приклад 11. Розв’язати рівняння 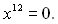
Розв’язання
Відповідь: 0.
Приклад 12. Розв’язати рівняння 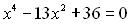 .
.
Розв’язання
Поклавши  , дістаємо
, дістаємо  . За теоремо Вієта
. За теоремо Вієта 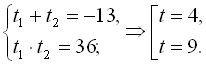
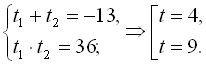
Відповідь: {±2; ±3}.
Приклад 13. Розв’язати рівняння 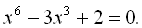
Розв’язання
Заміна 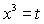 , одержимо
, одержимо  . Розкладемо ліву частину останнього рівняння на множники і повернемось до заміни:
. Розкладемо ліву частину останнього рівняння на множники і повернемось до заміни:
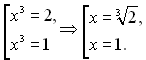
Відповідь: {1;  }.
}.
Приклад 14. Розв’язати рівняння 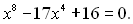
(Заміна 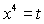 ).
).
Відповідь: {±1; ±2}.
Приклад 15. Розв’язати рівняння: 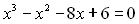 .
.
Розв’язання
Тут 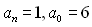 , тому, якщо дане рівняння має раціональні корені, то їх слід шукати серед дільників числа 6: ±1, ±2, ±3, ±6. Перевіркою дізнаємось, що
, тому, якщо дане рівняння має раціональні корені, то їх слід шукати серед дільників числа 6: ±1, ±2, ±3, ±6. Перевіркою дізнаємось, що 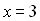 є коренем початкового рівняння. За теоремою Безу початковий многочлен ділиться без остачі на
є коренем початкового рівняння. За теоремою Безу початковий многочлен ділиться без остачі на 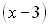 . Поділивши їх, отримаємо многочлен
. Поділивши їх, отримаємо многочлен 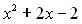 .
.
Таким чином,  . Тоді початкове рівняння набуває вигляду
. Тоді початкове рівняння набуває вигляду 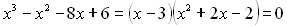 . Це рівняння рівносильне сукупності рівнянь:
. Це рівняння рівносильне сукупності рівнянь:  . Розв’язок першого рівняння
. Розв’язок першого рівняння  уже знайдений. Друге рівняння сукупності має корені
уже знайдений. Друге рівняння сукупності має корені 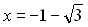 і
і  .
.
 . Розв’язок першого рівняння
. Розв’язок першого рівняння
Приклад 16. Розв’язати рівняння: 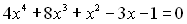 .
.
Розв’язання
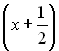 або, що те ж саме, але без дробів, на
або, що те ж саме, але без дробів, на  (тоді ми при діленні уникаємо дробових коефіцієнтів).
(тоді ми при діленні уникаємо дробових коефіцієнтів).
Як бачимо, множник 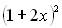 у другому степені, а це означає, що, використовуючи теорему Безу, нам потрібно ділити многочлен на множник
у другому степені, а це означає, що, використовуючи теорему Безу, нам потрібно ділити многочлен на множник  двічі.
двічі.
 двічі.
двічі.
Ми задавали дане рівняння з цілими коефіцієнтами, тому вираз 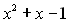 не розклався на множники, оскільки на раціональні множники він не розкладається. Розв’яжемо рівняння
не розклався на множники, оскільки на раціональні множники він не розкладається. Розв’яжемо рівняння 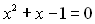 на множині ірраціональних чисел:
на множині ірраціональних чисел:
Розв’язуючи початкове рівняння, отримаємо:
Відповідь: 
Слід зазначити, що у випадку, коли ліва частина раціонального рівняння вищого степеня може бути розкладена на множники групуванням або яким-небудь іншим способом, розв’язок рівняння може бути отриманим більш простим шляхом.
Приклад 17. Розв’язати рівняння: 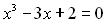 .
.
Розв’язання
Розкладемо один із членів даного тричлена на доданки: 
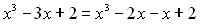 або
або 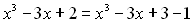 , тепер згрупуємо доданки зручним для нас способом, наприклад:
, тепер згрупуємо доданки зручним для нас способом, наприклад:
 або
або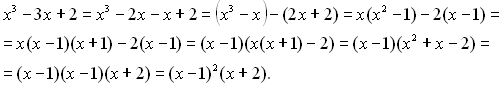
Отже,  , тоді
, тоді 

Відповідь: {-2; 1}.
Приклад 18. Розв’язати рівняння 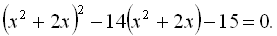
Розв’язання
Поклавши 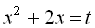 , дістанемо рівняння
, дістанемо рівняння 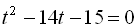 , звідки знаходимо
, звідки знаходимо 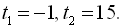 Тепер задача звелася до розв’язування сукупності рівнянь
Тепер задача звелася до розв’язування сукупності рівнянь 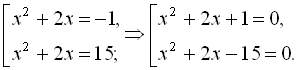 Перше рівняння сукупності має кратний корінь
Перше рівняння сукупності має кратний корінь 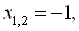 друге рівняння має корені
друге рівняння має корені  .
.
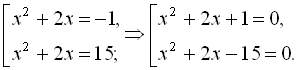 Перше рівняння сукупності має кратний корінь
Перше рівняння сукупності має кратний корінь
Відповідь: 
Приклад 19. Розв’язати рівняння 

Розв'язання
 .,
.,
Поклавши 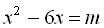 , дістанемо рівняння
, дістанемо рівняння 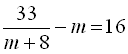 . Переносимо всі доданки рівняння в одну частину і зводимо до спільного знаменника:
. Переносимо всі доданки рівняння в одну частину і зводимо до спільного знаменника:
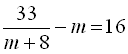 . Переносимо всі доданки рівняння в одну частину і зводимо до спільного знаменника:
. Переносимо всі доданки рівняння в одну частину і зводимо до спільного знаменника:
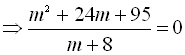
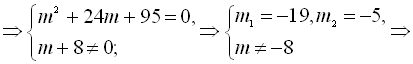
Узявши 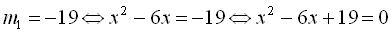 . Оскільки дискримінант цього рівняння
. Оскільки дискримінант цього рівняння 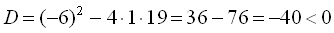 , то воно дійсних коренів не має.
, то воно дійсних коренів не має.
Узявши 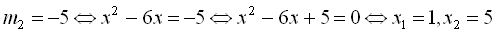 .
.
Отже, обидва корені є розв’язком нашого рівняння.
Відповідь: {1; 5}.
У дробово-раціональних рівняннях часто потрібно знаходити область допустимих значень (коротко ОДЗ). Її, як правило, знаходять на початку розв’язання прикладу. У попередньому прикладі натомість знаходження області допустимих значень ми застосували перевірку знайдених коренів.
Приклад 20. Розв’язати рівняння 

Розв'язання
Покладемо 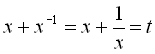 . До речі, ОДЗ:
. До речі, ОДЗ: 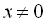 . Тоді
. Тоді
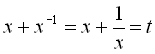 . До речі, ОДЗ:
. До речі, ОДЗ: 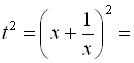

Початкове рівняння записується у вигляді 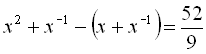
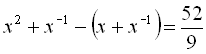
або 
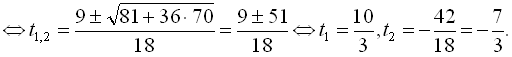

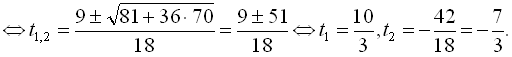
Узявши 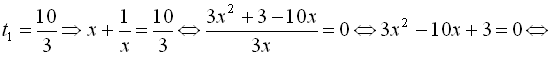
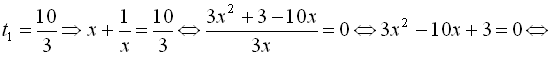
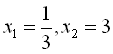 .
.
Узявши 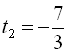 , дістаємо
, дістаємо 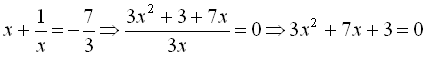
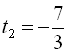 , дістаємо
, дістаємо 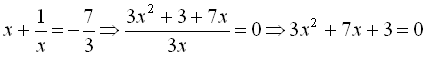

Відповідь: {
 3}.
3}.

Приклад 21. Розв’язати рівняння 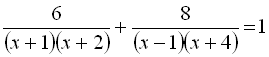 .
.
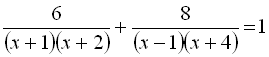 .
.
Розв'язання
Знайдемо ОДЗ:  та
та  або
або 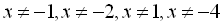 .
.
Розкриємо дужки у знаменниках дробів: 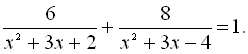 Як бачимо, можна зробити заміну
Як бачимо, можна зробити заміну  , тоді утворене рівняння буде мати вигляд:
, тоді утворене рівняння буде мати вигляд: 
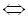
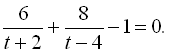
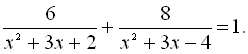 Як бачимо, можна зробити заміну
Як бачимо, можна зробити заміну 
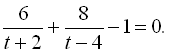
Тобто,  або
або 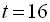 . Повертаємось до заміни:
. Повертаємось до заміни:  або
або 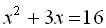 .
.
Отже, маємо такі розв’язки: 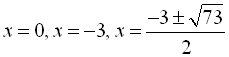 .
.
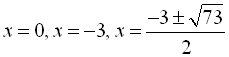 .
.
Всі отримані числа задовольняють ОДЗ, тому є коренями нашого рівняння.
Приклад 22. Розв’язати рівняння 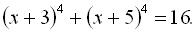
Розв'язання
Рівняння виду 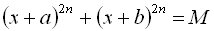
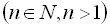 розв’язується за допомогою заміни
розв’язується за допомогою заміни  (с – середнє арифметичне чисел а і b). Для рівняння
(с – середнє арифметичне чисел а і b). Для рівняння 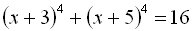
 робимо заміну
робимо заміну 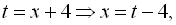
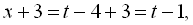
 (с – середнє арифметичне чисел а і b). Для рівняння
(с – середнє арифметичне чисел а і b). Для рівняння  робимо заміну
робимо заміну
Узявши 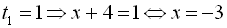 .
.
Узявши 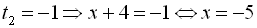 .
.
Відповідь: 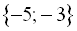 .
.
Приклад 23. Розв’язати рівняння: 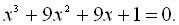
Розв’язання
Звідси
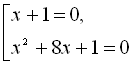
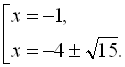
Відповідь: {-1; 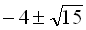 }.
}.
Приклад 24. Розв’язати рівняння: 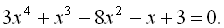
Розв’язання
Поділивши початкове рівняння на 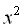 ,
, 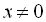 , дістаємо
, дістаємо
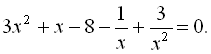 Згрупувавши доданки, маємо
Згрупувавши доданки, маємо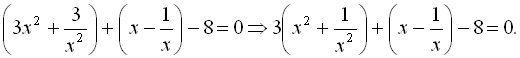
Поклавши 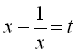 , маємо
, маємо 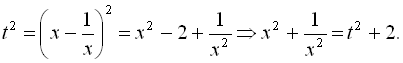
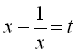 , маємо
, маємо 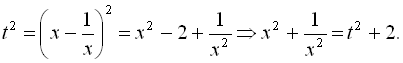
Таким чином, приходимо до рівняння
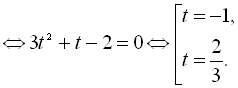
Повертаючись до заміни, маємо
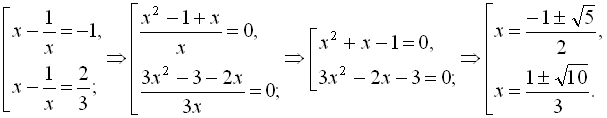
Відповідь: