Основні методи розв'язування систем рівнянь:
1) Метод підстановки. Спочатку за допомогою якого-небудь рівняння системи виражають одну змінну через іншу. Отриманий вираз підставляють в інше рівняння системи, в результаті чого приходять до рівняння з одною змінною, потім розв’язують це рівняння і знаходять відповідне значення іншої змінної.
2) Метод алгебраїчного додавання. При розв’язуванні системи цим методом переходять від даної системи до рівносильної їй системи, в якій одне з рівнянь містить лише одну змінну. При цьому звичайно множать одне або обидва рівняння на числові множники таким чином, щоб коефіцієнти при х або у були однаковими, але з протилежними знаками.
3) Метод введення нових змінних. Цей метод розв’язування систем розглянемо на прикладі 20.
Розв’язувати симетричну систему можна, наприклад, за допомогою заміни змінних, де новими змінними є основні симетричні многочлени.
Однорідні системи розв’язуються за допомогою застосування методів алгебраїчного додавання і введення нових змінних.
4) Графічний метод. Нехай, наприклад, потрібно розв’язати систему 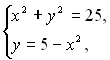 обидва рівняння якої є рівняннями другого степеня. Графіком рівняння
обидва рівняння якої є рівняннями другого степеня. Графіком рівняння 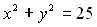 є коло, а графіком рівняння
є коло, а графіком рівняння 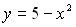 – парабола. Ці графіки мають три спільні точки:
– парабола. Ці графіки мають три спільні точки: 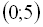 ,
, 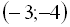 ,
, 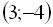 . Легко перевірити, що координати кожної з цих
. Легко перевірити, що координати кожної з цих 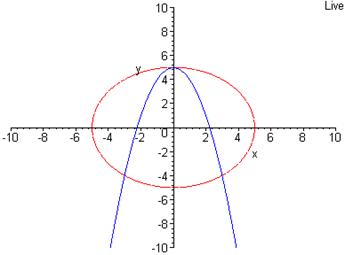 точок є розв’язком як першого, так і другого рівнянь системи. Тобто, система має 3 розв’язки. Отже, щоб розв’язати систему рівнянь із двома змінними графічним способом, потрібно побудувати графіки рівнянь системи в одній системі координат і знайти координати спільних точок цих графіків.
точок є розв’язком як першого, так і другого рівнянь системи. Тобто, система має 3 розв’язки. Отже, щоб розв’язати систему рівнянь із двома змінними графічним способом, потрібно побудувати графіки рівнянь системи в одній системі координат і знайти координати спільних точок цих графіків.
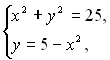 обидва рівняння якої є рівняннями другого степеня. Графіком рівняння
обидва рівняння якої є рівняннями другого степеня. Графіком рівняння  точок є розв’язком як першого, так і другого рівнянь системи. Тобто, система має 3 розв’язки. Отже, щоб розв’язати систему рівнянь із двома змінними графічним способом, потрібно побудувати графіки рівнянь системи в одній системі координат і знайти координати спільних точок цих графіків.
точок є розв’язком як першого, так і другого рівнянь системи. Тобто, система має 3 розв’язки. Отже, щоб розв’язати систему рівнянь із двома змінними графічним способом, потрібно побудувати графіки рівнянь системи в одній системі координат і знайти координати спільних точок цих графіків.
Але цей спосіб не є основним способом розв’язування рівнянь, тому що він не завжди дає точні результати.
Приклади систем рівнянь та їх розв’язування:
Приклад 25. Розв’язати систему рівнянь 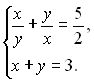
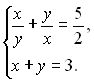
Розв’язання
1-й спосіб розв’язування:
Розв’яжемо дану систему рівнянь методом підстановки, для цього з другого рівняння системи визначимо у і підставимо його у перше рівняння:
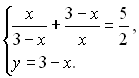
Розв’яжемо перше рівняння отриманої системи: 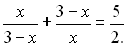
Перенесемо 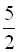 у ліву частину і зведемо вираз до спільного знаменника:
у ліву частину і зведемо вираз до спільного знаменника:
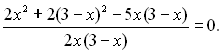
За умови, що знаменник 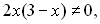 маємо:
маємо:
Зведемо подібні: 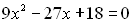
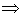
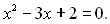
За теоремою Вієта: 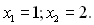
Отже, 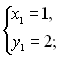 або
або 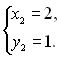
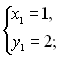 або
або 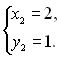
2-й спосіб розв’язування:
У першому рівнянні системи 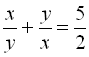 зробимо заміну
зробимо заміну 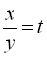 , тоді
, тоді
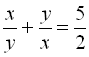 зробимо заміну
зробимо заміну 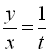 . Одержуємо рівняння
. Одержуємо рівняння 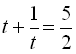
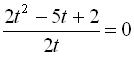
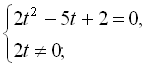
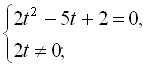
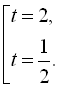 Повернемось до заміни:
Повернемось до заміни: 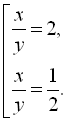
Враховуючи друге рівняння початкової системи, отримаємо сукупність двох систем:
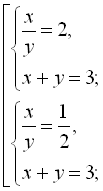
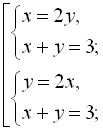
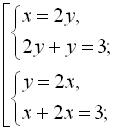
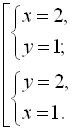
Відповідь: (1; 2), (2; 1).
Приклад 26. Розв’язати систему рівнянь 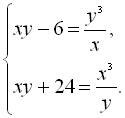
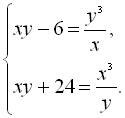
Розв’язання
Розв’яжемо дану систему методом алгебраїчного додавання, для цього перемножимо рівняння системи і одержимо:
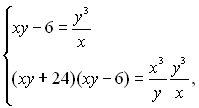 (1)
(1)
Друге рівняння отриманої системи шляхом нескладних перетворень зводиться до рівняння 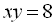 – наслідку другого рівняння системи (1). Тоді система
– наслідку другого рівняння системи (1). Тоді система 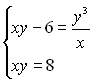 (2) буде наслідком системи (1).
(2) буде наслідком системи (1).
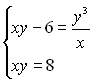 (2) буде наслідком системи (1).
(2) буде наслідком системи (1).
Віднімемо тепер перше рівняння системи (2) від другого. Отримаємо систему 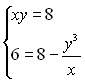 або
або 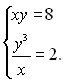 (3)
(3)
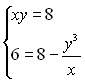 або
або 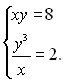 (3)
(3)
Система (3) – наслідок системи (2).
Перемножимо рівняння системи (3) і отримаємо систему
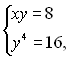 (4)
(4)
яка буде наслідком системи (3). З другого рівняння системи (4) знаходимо 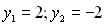 , а з першого рівняння, відповідно,
, а з першого рівняння, відповідно, 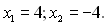
Таким чином, система (4) має такі розв'язки:
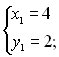 або
або 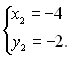
Відповідь: (4; 2), (-4; -2).
Приклад 27. Розв'язати систему рівнянь 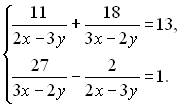
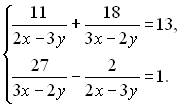
Розв'язання
Розв’яжемо дану систему методом заміни змінної:
Позначимо 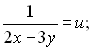
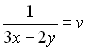 .
.
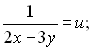
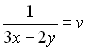 .
.
Зробивши заміну, дістанемо нову систему:
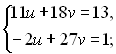 або
або 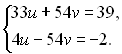
Повернемось до попередніх змінних:
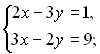
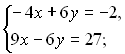
Відповідь: (5; 3).
Приклад 28. Задача на знаходження числа
Приклад 28. Задача на знаходження числа
Знайти двоцифрове число, яке при діленні на добуток його цифр дає частку 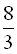 , а різниця між ним та числом з переставленими цифрами дорівнює 18.
, а різниця між ним та числом з переставленими цифрами дорівнює 18.
Розв’язання
Позначимо через x та y першу і другу цифри, тоді невідоме число матиме вигляд 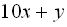 , а число з переставленими цифрами
, а число з переставленими цифрами 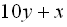 . Запишемо систему рівнянь
. Запишемо систему рівнянь 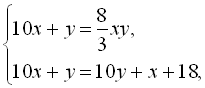 звідки знаходимо:
звідки знаходимо: 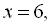
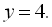 Отже,
Отже, 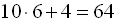 – шукане число.
– шукане число.
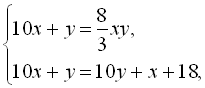 звідки знаходимо:
звідки знаходимо:
Відповідь: 64.
