Арифметичною прогресією називається числова послідовність, кожний член якої, починаючи з другого, дорівнює попередньому, доданому до того ж самого постійного для даної послідовності числа. Позначається арифметична прогресія звичайно 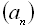 .
. 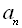 називається n-м членом арифметичної прогресії.
називається n-м членом арифметичної прогресії.
З визначення арифметичної прогресії випливає, що 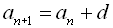 . Число d називається різницею прогресії. Таким чином
. Число d називається різницею прогресії. Таким чином
Для того, щоб задати арифметичну прогресію 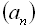 , достатньо знати її перший член
, достатньо знати її перший член 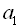 і різницю d. Якщо різниця арифметичної прогресії – додатне число, то така прогресія є зростаючою; якщо різниця є від’ємним числом, то спадною. Якщо різниця d арифметичної прогресії дорівнює нулю, то всі члени прогресії рівні між собою.
і різницю d. Якщо різниця арифметичної прогресії – додатне число, то така прогресія є зростаючою; якщо різниця є від’ємним числом, то спадною. Якщо різниця d арифметичної прогресії дорівнює нулю, то всі члени прогресії рівні між собою.
Характеристичні властивості арифметичної прогресії:
а) кожний член арифметичної прогресії, починаючи з другого, є середнім арифметичним сусідніх з ним членів:
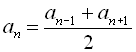 ,
,
б) сума членів, рівновіддалених від кінців прогресії, є величиною сталою, тобто
Формула п-го члена арифметичної прогресії має вигляд:
Формула для суми п перших членів арифметичної прогресії має вигляд
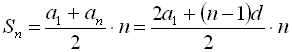 .
.
Геометричною прогресією називається така числова послідовність 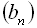 , кожний член якої, починаючи з другого, дорівнює попередньому, помноженому на те ж саме стале для даної послідовності число, відмінне від нуля. Перший член геометричної прогресії передбачається відмінним від нуля.
, кожний член якої, починаючи з другого, дорівнює попередньому, помноженому на те ж саме стале для даної послідовності число, відмінне від нуля. Перший член геометричної прогресії передбачається відмінним від нуля. 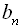 називається п-им членом геометричної прогресії.
називається п-им членом геометричної прогресії.
З визначення геометричної прогресії випливає, що 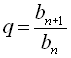 . Число
. Число 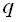
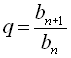 . Число
. Число
називається знаменником геометричної прогресії. Таким чином,
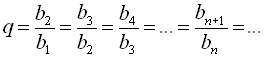 .
.
Для того, щоб задати геометричну прогресію 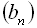 , достатньо знати її перший член і знаменник.
, достатньо знати її перший член і знаменник.
Якщо 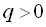 і
і 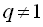 , то геометрична прогресія є монотонною послідовністю. Якщо
, то геометрична прогресія є монотонною послідовністю. Якщо 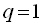 , то всі члени прогресії рівні між собою. У цьому випадку геометрична прогресія є сталою послідовністю, яка розглядається рідко.
, то всі члени прогресії рівні між собою. У цьому випадку геометрична прогресія є сталою послідовністю, яка розглядається рідко.
Характеристичні властивості геометричної прогресії формулюються в такий спосіб:
а) у геометричній прогресії, усі члени якої додатні числа, будь-який її член, починаючи з другого, є середнім геометричним сусідніх з ним членів, тобто при 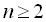
б) добуток членів, рівновіддалених від кінців геометричної прогресії, є величиною сталою, тобто
Формула п-го члена геометричної прогресії має вигляд
Формула для суми п перших членів геометричної прогресії має вигляд 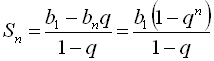 .
.
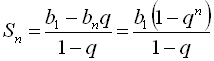 .
.
Нескінченно спадною геометричною прогресією називають таку геометричну прогресію 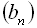 , у якої знаменник
, у якої знаменник 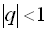 і яка містить нескінченне число доданків. Сума нескінченно спадної геометричної прогресії обчислюється за формулою
і яка містить нескінченне число доданків. Сума нескінченно спадної геометричної прогресії обчислюється за формулою 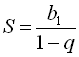 .
.
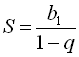 .
.
Приклад 1. Знайти одинадцятий член арифметичної прогресії 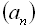 , якщо її перший член дорівнює
, якщо її перший член дорівнює 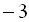 , а різниця цієї прогресії рівна 0,7.
, а різниця цієї прогресії рівна 0,7.
Розв’язання
За умовою, 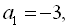
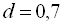 . Для знаходження одинадцятого члена арифметичної прогресії, скористаємось формулою п-го члена арифметич-ної прогресії
. Для знаходження одинадцятого члена арифметичної прогресії, скористаємось формулою п-го члена арифметич-ної прогресії 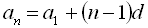 . Тобто
. Тобто 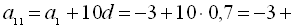 7=4.
7=4.
Відповідь: 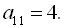
Приклад 2. Різниця арифметичної прогресії дорівнює 3, а сума перших її шести членів дорівнює 57. Знайти перший та шостий члени прогресії.
Розв’язання
За умовою 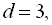
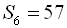 . Скористаємось формулою для суми п перших членів арифметичної прогресії
. Скористаємось формулою для суми п перших членів арифметичної прогресії 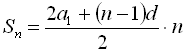 . Маємо
. Маємо 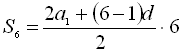 , отже
, отже
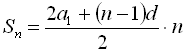 . Маємо
. Маємо 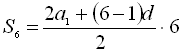 , отже
, отже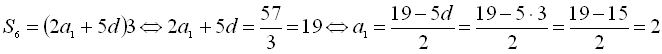 .
.
Відповідь: 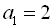 ;
; 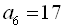 .
.
Приклад 3. Знайти арифметичну прогресію 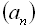 , якщо
, якщо 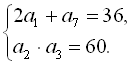
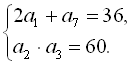
Розв’язання
Розпишемо другий, третій та сьомий члени прогресії через перший її член та різницю. Тобто 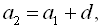
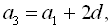
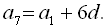 Підставивши отримані дані у початкову систему, дістаємо:
Підставивши отримані дані у початкову систему, дістаємо:
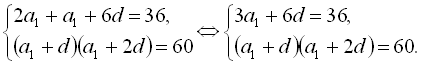
З першого рівняння системи 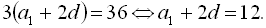 Підставивши це значення в друге рівняння системи, дістаємо
Підставивши це значення в друге рівняння системи, дістаємо 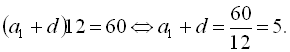 Звідси маємо рівносильну початкову систему
Звідси маємо рівносильну початкову систему 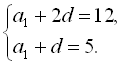 Від першого рівняння системи віднімемо друге рівняння і отримаємо:
Від першого рівняння системи віднімемо друге рівняння і отримаємо: 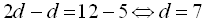 . Тоді
. Тоді 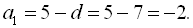
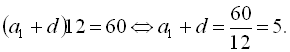 Звідси маємо рівносильну початкову систему
Звідси маємо рівносильну початкову систему 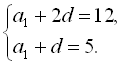 Від першого рівняння системи віднімемо друге рівняння і отримаємо:
Від першого рівняння системи віднімемо друге рівняння і отримаємо:
Відповідь: 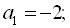
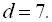
Приклад 4. Знайти суму всіх додатних парних трицифрових чисел, що діляться на 3 без остачі.
Розв’язання
Додатні парні трицифрові числа: 100, 102, 104, 106, 108, …, 994, 996, 998. З них тих, що діляться на 3: 102, 108, 114, …, 990, 996. Отримана числова послідовність є арифметичною прогресією з різницею 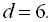 Значить
Значить 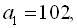
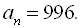 За формулою п-го члена знаходимо число членів даної прогресії
За формулою п-го члена знаходимо число членів даної прогресії 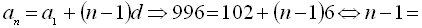 149
149
Отже, шукану суму знаходимо за формулою 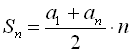 . Значить
. Значить 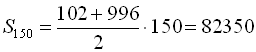 .
.
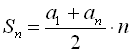 . Значить
. Значить 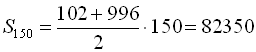 .
.
Відповідь: 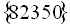 .
.
Приклад 5. Знайти арифметичну прогресію, якщо сума її п перших членів 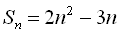 .
.
Розв’язання
Випишемо кілька перших членів даної прогресії: -1; 3; 7; 11; … .
Відповідь: 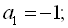
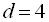 .
.
Приклад 6. Перший член геометричної прогресії дорівнює 16, а її знаменник рівний 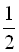 . Знайти сьомий член прогресії.
. Знайти сьомий член прогресії.
Розв’язання
За умовою, 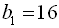 ;
; 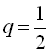 . Для знаходження сьомого члена даної прогресії скористаємося формулою п-го члена геометричної прогресії
. Для знаходження сьомого члена даної прогресії скористаємося формулою п-го члена геометричної прогресії 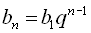 . Отже,
. Отже, 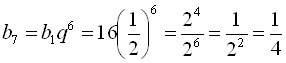 .
.
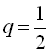 . Для знаходження сьомого члена даної прогресії скористаємося формулою п-го члена геометричної прогресії
. Для знаходження сьомого члена даної прогресії скористаємося формулою п-го члена геометричної прогресії 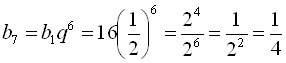 .
.
Відповідь: 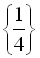 .
.
Приклад 7. Дана геометрична прогресія 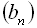 : -2; 8; -32; 128; … . Знайти
: -2; 8; -32; 128; … . Знайти 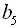 .
.
Розв’язання
Знаходимо спочатку знаменник прогресії: 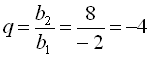 ;
; 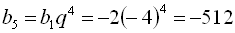 .
.
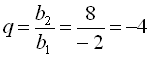 ;
;
Відповідь: 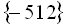 .
.
Приклад 8. У геометричній прогресії 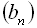
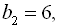
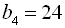 . Знайти
. Знайти 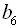 .
.
Розв’язання
Знайдемо спочатку знаменник прогресій q. За умовою 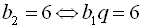 ;
; 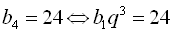 ;
; 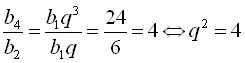 ;
;
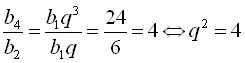 ;
;
Відповідь: 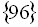 .
.
Приклад 9. Знайти суму 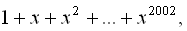
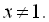
Розв’язання
Маємо 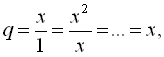
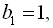
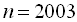 . Шукану суму знаходимо за формулою суми п перших членів геометричної прогресії
. Шукану суму знаходимо за формулою суми п перших членів геометричної прогресії 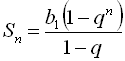 , тобто
, тобто 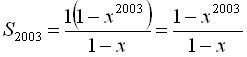 .
.
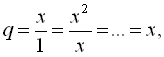
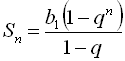 , тобто
, тобто 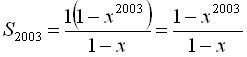 .
.
Відповідь: 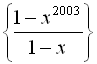 .
.
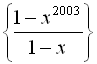 .
.
Приклад 10. У геометричній прогресії 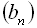 :
: 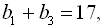
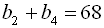 . Знайти
. Знайти 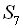 .
.
Розв’язання
Оскільки 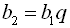 ,
, 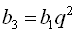 ,
, 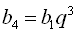 , то складемо таку систему рівнянь:
, то складемо таку систему рівнянь: 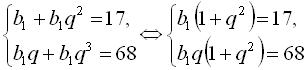 . Поділивши почленно друге рівняння на перше, дістанемо
. Поділивши почленно друге рівняння на перше, дістанемо 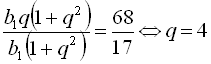 . З першого рівняння системи
. З першого рівняння системи 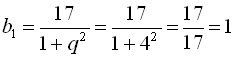 . Отже,
. Отже, 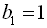 ,
, 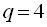 . За формулою для суми п перших членів знаходимо
. За формулою для суми п перших членів знаходимо 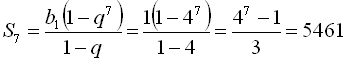 .
.
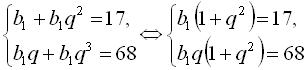 . Поділивши почленно друге рівняння на перше, дістанемо
. Поділивши почленно друге рівняння на перше, дістанемо 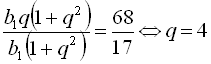 . З першого рівняння системи
. З першого рівняння системи 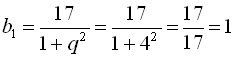 . Отже,
. Отже, 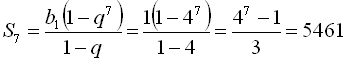 .
.
Відповідь: 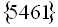 .
.
Приклад 11. Число членів геометричної прогресії парне, сума всіх членів цієї прогресії в три рази більша від суми її членів, які стоять на непарних місцях. Знайдіть знаменник прогресії.
Розв’язання
Нехай задано геометричну прогресію 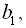
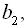 …,
…, 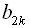 , яка має парне число членів. Сума цієї прогресії –
, яка має парне число членів. Сума цієї прогресії – 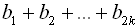 в три рази більша від суми членів, які стоять на непарних місцях, тобто в три рази більша від
в три рази більша від суми членів, які стоять на непарних місцях, тобто в три рази більша від 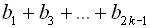 . Отже,
. Отже, 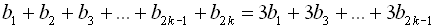 ;
;
Запишемо кожний елемент прогресії через 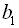 і
і 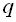 , тоді
, тоді
Відповідь: 2.
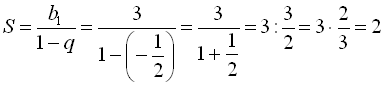 .
.
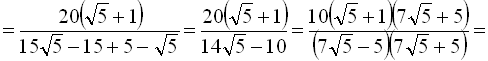
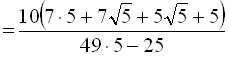
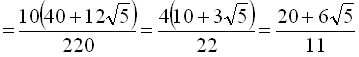 .
.
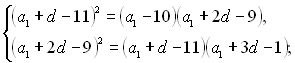
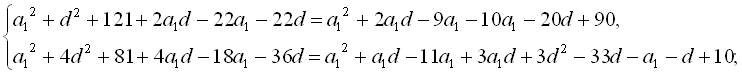
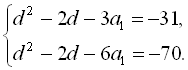 Віднявши від першого рівняння останньої системи друге рівняння, отримаємо
Віднявши від першого рівняння останньої системи друге рівняння, отримаємо 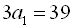 ,
, 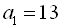 . Тоді
. Тоді 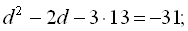
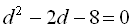 . Звідси
. Звідси 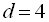 або
або 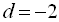 .
.
Приклад 12. Знайти суму нескінченно спадної геометричної прогресії:
1) 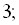
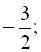

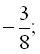 … ;
… ;
2) 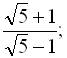
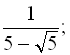
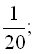 … .
… .
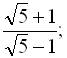
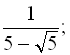
Розв’язання
1) З умови зрозуміло, що 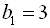 ,
,  . Тоді
. Тоді
 . Тоді
. Тоді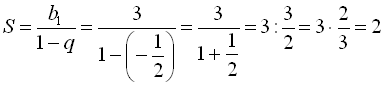 .
.
2) З умови зрозуміло, що 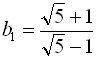 ,
, 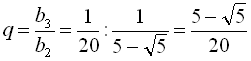 . Тоді
. Тоді 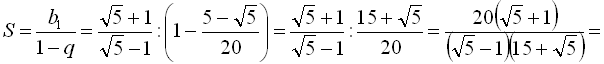
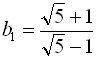 ,
, 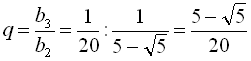 . Тоді
. Тоді 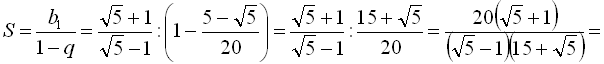
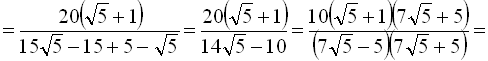
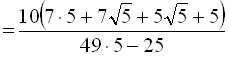
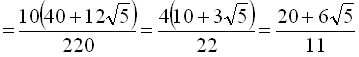 .
.
Відповідь: 1) 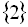 ; 2)
; 2) 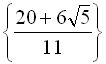 .
.
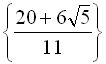 .
.
Приклад 13. Сума нескінченно спадної геометричної прогресії 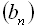
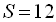 , а сума квадратів усіх її членів
, а сума квадратів усіх її членів 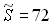 . Знайти п’ятий член прогресії.
. Знайти п’ятий член прогресії.
Розв’язання
Прогресія, у якої кожним членом є квадрат 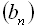 , тобто
, тобто 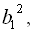
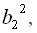
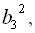
…, 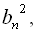 … має знаменник
… має знаменник 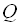 , який дорівнює квадрату знаменника заданої прогресії
, який дорівнює квадрату знаменника заданої прогресії 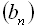 , тому що
, тому що  . Звідси маємо систему рівнянь
. Звідси маємо систему рівнянь 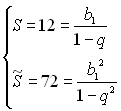 . Поділивши друге рівняння системи на перше, піднесене до квадрата, дістанемо
. Поділивши друге рівняння системи на перше, піднесене до квадрата, дістанемо 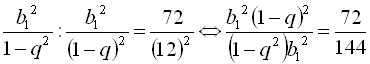 .
.
 . Звідси маємо систему рівнянь
. Звідси маємо систему рівнянь 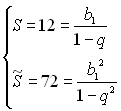 . Поділивши друге рівняння системи на перше, піднесене до квадрата, дістанемо
. Поділивши друге рівняння системи на перше, піднесене до квадрата, дістанемо 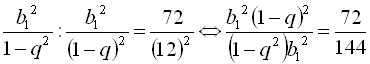 .
.
З отриманої рівності, маємо 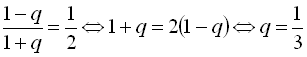 .
.
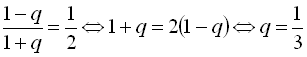 .
.
Тоді 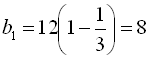 ;
; 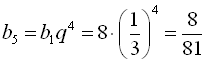 .
.
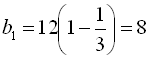 ;
; 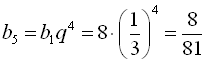 .
.
Відповідь: 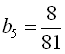 .
.
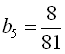 .
.
Приклад 14. Чотири числа становлять арифметичну прогресію. Якщо від них відняти відповідно 10, 11, 9 і 1, то нові числа становитимуть геометричну прогресію. Знайдіть ці числа.
Розв’язання
Нехай 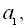
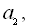
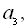
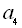 – члени арифметичної прогресії або
– члени арифметичної прогресії або 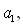
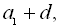
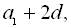
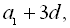 де d – різниця прогресії. За умовою
де d – різниця прогресії. За умовою 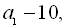
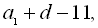
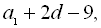
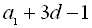 – члени геометричної прогресії.
– члени геометричної прогресії.
За властивістю геометричної прогресії складено систему рівнянь:
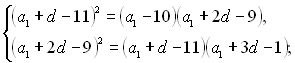
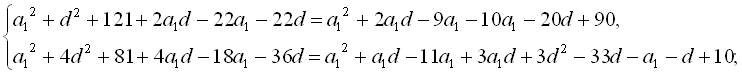
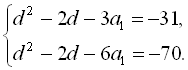 Віднявши від першого рівняння останньої системи друге рівняння, отримаємо
Віднявши від першого рівняння останньої системи друге рівняння, отримаємо
Якщо 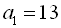 і
і 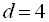 , то числа 13, 17, 21 і 25 – члени арифметичної прогресії, а числа 3, 6, 12, 24 – члени геометричної прогресії.
, то числа 13, 17, 21 і 25 – члени арифметичної прогресії, а числа 3, 6, 12, 24 – члени геометричної прогресії.
Якщо 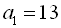 і
і 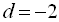 , то числа 13, 11, 9 і 7 – члени арифметичної прогресії, а числа 3, 0, 0, 6 – не є членами геометричної прогресії.
, то числа 13, 11, 9 і 7 – члени арифметичної прогресії, а числа 3, 0, 0, 6 – не є членами геометричної прогресії.
Відповідь: 13, 17, 21 і 25.
Приклад 15. Розв’язати рівняння 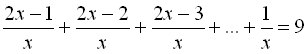 ,
, 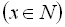 .
.
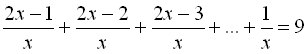 ,
,
Розв’язання
Підказка. Зверніть увагу, що доданки в рівнянні є членами арифметичної прогресії, тобто ліва частина рівняння – це сума перших 2х - 1 членів прогресії. Відповідь: 5.
