Дроби бувають звичайні і десяткові. Звичайні дроби бувають правильні і неправильні. 

Звичайні дроби можна скорочувати, додавати, віднімати множити і ділити. 

Бувають так звані мішані числа. Вони складаються з цілої і дробової частини

(за замовчуванням дробова частина мішаного числа є правильним дробом).

Є чимало тонкощів і деталей, про які варто знати. 

При розв‘язуванні вправ досить часто доводиться працювати з усіма видами дробів, тому потрібно знати, як їх поєднувати.

Основна властивість звичайного дробу
Якщо чисельник і знаменник дробу помножити або поділити
на одне й те саме число, відмінне від нуля,
то отримаємо дріб, який рівний даному.

Наприклад,

Процес ділення чисельника і знаменника на одне й те саме число, відмінне від нуля, називають скороченням дробу, бо всі числа при цьому зменшуються.

Інколи доводиться робити протилежну дію: перетворювати мішане число в неправильний дріб.

При додаванні (відніманні) дробів з однаковими знаменниками до чисельника першого дробу додають чисельник другого дробу (від чисельника першого дробу віднімають чисельник другого дробу) і залишають той же знаменник. Отриманий дріб, якщо це можливо, скорочують. 

Наприклад, ,    .

При додаванні (відніманні) дробів з різними знаменниками cпочатку потрібно 
звести їх до найменшого спільного знаменника, а потім виконувати дію так, як описано вище. 
Наприклад,  .    

При додаванні мішаних чисел потрібно додати окремо цілі частини і дробові частини. 
Наприклад, .

При відніманні мішаних чисел варто розрізняти такі випадки:

a) дробова частина зменшуваного більша або дорівнює дробовій частині від’ємника; у цьому випадку від цілої частини зменшуваного віднімають цілу частину від’ємника, а від дробової частини зменшуваного – дробову частину від’ємника.
Наприклад, 

б) дробова частина зменшуваного менша від дробової частини від’ємника; в цьому випадку одну з одиниць цілої частини зменшуваного потрібно замінити таким дробом, який їй дорівнює. Наприклад, 

Множення звичайних дробів виконується таким чином: , тобто перемножують окремо чисельники, окремо знаменники. Перший добуток роблять чисельником, другий – знаменником. Отриманий дріб, якщо це можливо, скорочують.

При множенні мішаних чисел їх попередньо перетворюють у неправильні дроби, а потім перемножують. 
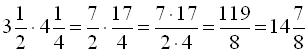Наприклад, .

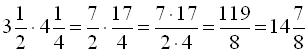При діленні дробу на дріб чисельник діленого множать на знаменник дільника, а знаменник діленого – на чисельник дільника. Перший добуток служить чисельником частки, а другий – її знаменником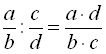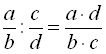: . Наприклад, .

Якщо потрібно поділити мішані числа, то спочатку перетворюють їх  у неправильний дріб.

Будь-яке ціле число можна зобразити у вигляді дробу з яким завгодно знаменником. Наприклад,   

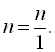
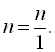
Два числа називаються взаємно оберненими, якщо їхній добуток дорівнює 1.
Наприклад,