Універсальний метод (метод інтервалів (проміжків)) при розв’язуванні рівнянь з модулями
Даний метод полягає в тому, що:
1) вирази, які стоять під знаком модуля, прирівнюються до нуля;
2) отримані значення відкладаються на числовій прямій, яка при цьому розбивається на інтервали (проміжки), в кожному з яких свій знак підмодулевого виразу;
3) розв’язуються отримані рівняння в кожному з інтервалів.
На практиці метод інтервалів зазвичай застосовується тоді, коли рівняння містить декілька модулів.
Розглянемо застосування методу інтервалів на прикладах.
Приклад 1. Розв’язати рівняння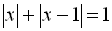 
.
.Розв’язання
1-й спосіб розв’язування:
; 
. Наносимо на числову пряму точки 
і 
. Ці точки розбивають числову пряму на три інтервали (проміжки), у кожному з яких свій знак підмодулевого виразу. Для зручності можна позначити ці інтервали І, ІІ, ІІІ:
І: 
; ІІ: 
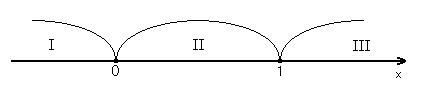
; І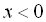ІІ: 
.
; ІІ: 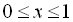; ІІІ: 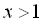.Для інтервалу І маємо: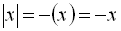 
; 
.
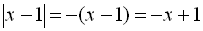; . Звідси, дістаємо розв’язання рівняння в І інтервалі: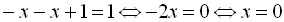 
. Однак значення 
не належить І інтервалу, тобто 
, тому в І інтервалі початкове рівняння розв'язків не має.
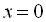. Однак значення не належить І інтервалу, тобто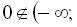 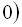, тому в І інтервалі початкове рівняння 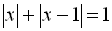розв'язків не має. Для ІІ інтервалу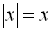 
; 
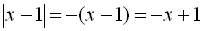
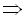початкове рівняння має вигляд 
. Оскільки 
– це тотожність, то будь-яке 
є розв’язком, тобто розв’язком рівняння є весь відрізок 
.
; початкове рівняння має вигляд 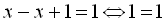. Оскільки 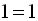– це тотожність, то будь-яке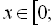 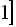є розв’язком, тобто розв’язком рівняння є весь відрізок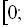 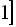. Для ІІІ інтервалу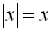 
; 
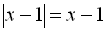
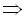початкове рівняння має вигляд: 
. Оскільки 
, то в ІІІ інтервалі початкове рівняння розв’язків не має.
; початкове рівняння має вигляд: 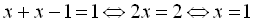. Оскільки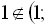 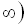, то в ІІІ інтервалі початкове рівняння розв’язків не має.2-й спосіб розв’язування:
Розв’язання даного прикладу можна записати в іншій формі, застосовуючи поняття сукупності змішаних систем, тобто систем, які містять рівняння і нерівності.
Так само, як і для 1-го способу, маємо три інтервали: 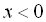І: ; ІІ: 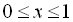; ІІІ: 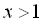. В залежності від того, у якому інтервалі ми шукаємо розв’язок, початкове рівняння рівносильне сукупності таких змішаних систем: 
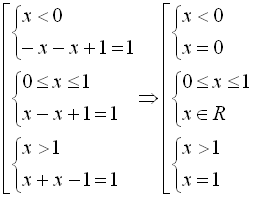. Перша і третя системи сукупності розв’язків не мають, а розв’язком другої системи є проміжок 
.
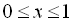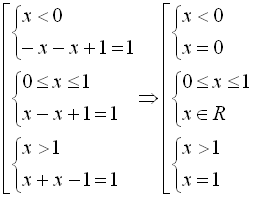; ІІ: ; ІІІ: . В залежності від того, у якому інтервалі ми шукаємо розв’язок, початкове рівняння рівносильне сукупності таких змішаних систем: . Перша і третя системи сукупності розв’язків не мають, а розв’язком другої системи є проміжок .Відповідь: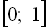 
.
.Приклад 2. Розв’язати рівняння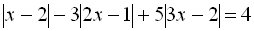 
.
.Розв’язання
Рівняння з трьома і більше модулями зручно розв’язувати лише методом інтервалів.
; 
; 
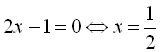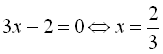.Маємо чотири інтервали:
І: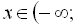 
;
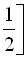;ІІ: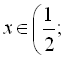 
;
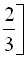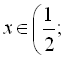
;ІІІ: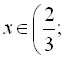 
;
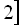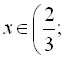
;ІV: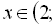 
.
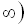.У І інтервалі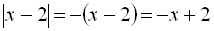 
, 
, 
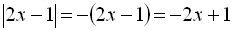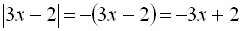. Звідси, маємо
, , . Звідси, маємо
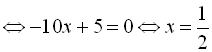. Оскільки 
входить в інтервал 
, то 
є розв’язком початкового рівняння.У ІІ інтервалі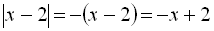 
; 
; .
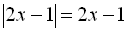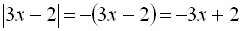; ; .Тоді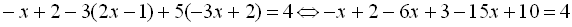 
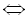
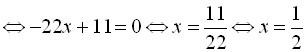. Однак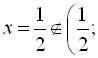 
.Для ІІІ інтервалу ; ;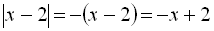 
.
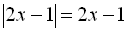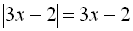; ; .Звідси маємо
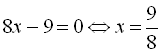. Тому що 
входить в інтервал 
, то 
є розв’язком початкового рівняння.Для ІV інтервалу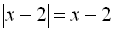 
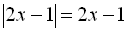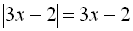; ; . Звідси дістаємо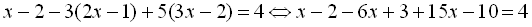 
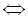
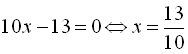. Однак значення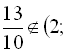 
.
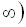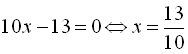; ; . Звідси дістаємо . Однак значення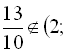 .Відповідь: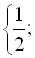 
.
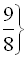.Приклад 3. Розв’язати систему рівнянь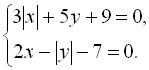 
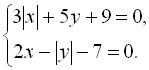
Розв’язання
В даному випадку областю допустимих значень для x і y є множина всіх дійсних чисел.
Замінимо дану систему рівнянь еквівалентною сукупністю систем: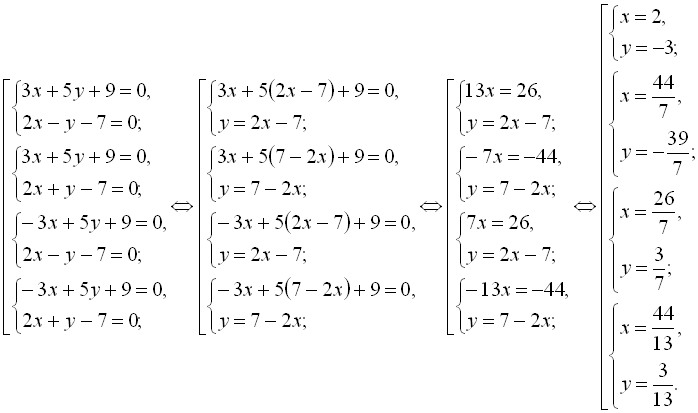
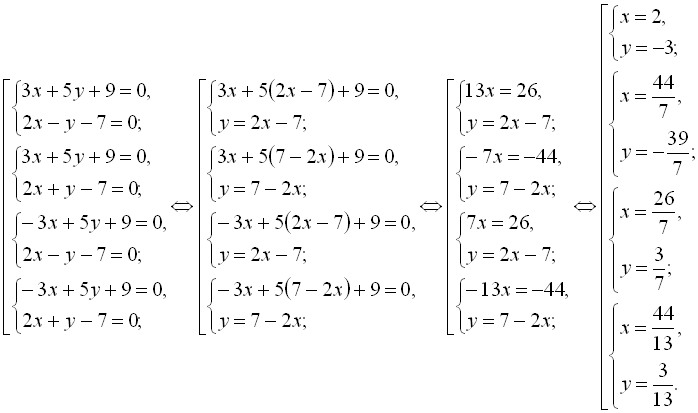
В даному прикладі робити перевірку – рутинна робота.
Як бачимо, три пари чисел, які отримали при розв’язанні даної системи, виявились сторонніми.
Відповідь: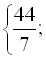 
.
.
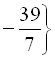
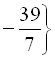