Розв’язування задач на складання рівнянь можна розбити на кілька етапів:
1) вибір невідомих величин і їх позначення,
2) запис вказаних співвідношень у вигляді рівнянь або систем рівнянь,
3) розв’язання цих рівнянь або системи рівнянь з урахуванням області визначення
(при цьому враховуються природні фізичні обмеження, які звичайно в тексті задач не наведено).
1) вибір невідомих величин і їх позначення,
2) запис вказаних співвідношень у вигляді рівнянь або систем рівнянь,
3) розв’язання цих рівнянь або системи рівнянь з урахуванням області визначення
(при цьому враховуються природні фізичні обмеження, які звичайно в тексті задач не наведено).
Відстань від пункту А до пункту Б залізницею дорівнює 105 км, а річкою – 150 км. Поїзд з пункту А виходить на 2 години пізніше від теплохода і прибуває до пункту Б на 15 хвилин раніше. Знайдіть швидкість (у кілометрах за годину) поїзда, якщо вона на 30 км/год більша за швидкість теплохода.
Розв’язання
Позначимо швидкість руху теплохода через х, тоді швидкість поїзда дорівнюватиме х+30. Час руху теплохода дорівнює 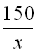 , а поїзда –
, а поїзда – 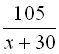 . За умовою задачі, поїзд з пункту А виходить на 2 години пізніше від теплохода і прибуває до пункту Б на 15 хвилин раніше, то різниця у часі між теплоходом і поїздом становить 2 год 15 хв., або
. За умовою задачі, поїзд з пункту А виходить на 2 години пізніше від теплохода і прибуває до пункту Б на 15 хвилин раніше, то різниця у часі між теплоходом і поїздом становить 2 год 15 хв., або 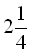 год. Отже, можна скласти рівняння
год. Отже, можна скласти рівняння 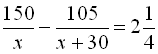 . Розв’яжемо дане рівняння:
. Розв’яжемо дане рівняння:
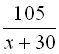 . За умовою задачі, поїзд з пункту А виходить на 2 години пізніше від теплохода і прибуває до пункту Б на 15 хвилин раніше, то різниця у часі між теплоходом і поїздом становить 2 год 15 хв., або
. За умовою задачі, поїзд з пункту А виходить на 2 години пізніше від теплохода і прибуває до пункту Б на 15 хвилин раніше, то різниця у часі між теплоходом і поїздом становить 2 год 15 хв., або 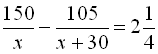 . Розв’яжемо дане рівняння:
. Розв’яжемо дане рівняння: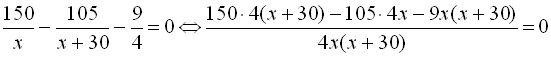 .
.Областю допустимих значень даного рівняння є 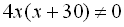 , звідси
, звідси 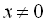 та
та 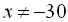 , що і так не можливо згідно з умовою задачі. Тоді прирівняємо чисельник останнього рівняння до нуля
, що і так не можливо згідно з умовою задачі. Тоді прирівняємо чисельник останнього рівняння до нуля 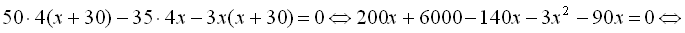
Відповідь: 70 км/год.

